Trinômio do quadrado perfeito é o 3º caso de fatoração de expressão algébrica. Ele só pode ser utilizado quando a expressão algébrica for um trinômio (polinômio com três monômios) e esse trinômio formar um quadrado perfeito.
O que é trinômio
Trinômio é um polinômio que tem três monômios sem termos semelhantes, veja exemplos:
3x2 + 2x + 1
20x3 + 5x – 2x2
2ab +5b + 3c
Nem todos os trinômios acima podem ser fatorados utilizando o quadrado perfeito.
O que é quadrado perfeito
Para melhor entender o que é quadrado perfeito, veja:
Podemos considerar um número sendo quadrado perfeito? Sim, basta que esse número seja o resultado de outro número elevado ao quadrado, por exemplo: 25 é um quadrado perfeito, pois 52 = 25.
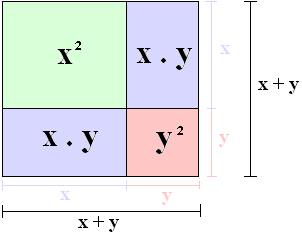
Agora, devemos aplicar isso em uma expressão algébrica, observe o quadrado abaixo com lados x + y, o valor desse lado é uma expressão algébrica.
Para calcularmos a área desse quadrado podemos seguir duas formas diferentes:
1º forma: a fórmula para o cálculo da área do quadrado é A = Lado2 , então, como o lado nesse quadrado é x + y, basta elevá-lo ao quadrado.
A1 = (x + y)2
O resultado dessa área A1 = (x + y)2 é um quadrado perfeito.
2º forma: esse quadrado foi dividido em quatro retângulos onde cada um tem a sua própria área, então a soma de todas essas áreas é a área total do quadrado maior, ficando assim:
A2 = x2 + xy + xy + y2, como xy e xy são semelhantes podemos somá-los
A2 = x2 +2xy + y2
O resultado da área A2 = x2 +2xy + y2 é um trinômio.
As duas áreas encontradas representam a área do mesmo quadrado, então:
A1 = A2
(x + y)2 = x2 +2xy + y2
Então, o trinômio x2 +2xy + y2 tem como quadrado perfeito (x + y)2.
Quando tivermos uma expressão algébrica e ela for um trinômio do quadrado perfeito a sua forma fatorada é representada em forma de quadrado perfeito, veja:
O trinômio x2 +2xy + y2 fatorado fica (x + y)2.
Como identificar um trinômio do quadrado perfeito
Como já foi dito, nem todo trinômio pode ser representado na forma de quadrado perfeito. Agora, quando é dado um trinômio como iremos identificar que é quadrado perfeito ou não?
Para que um trinômio seja quadrado perfeito ele deve ter algumas características:
• Dois termos (monômios) do trinômio devem ser quadrados.
• Um termo (monômio) do trinômio deve ser o dobro das raízes quadradas dos dois outros termos.
Veja um exemplo:
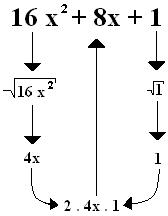
Veja se o trinômio 16x2 + 8x + 1 é um quadrado perfeito, para isso siga as regras acima:
Dois membros do trinômio têm raízes quadradas e o dobro delas é o termo do meio, então o trinômio 16x2 + 8x + 1 é quadrado perfeito.
Então, a forma fatorada do trinômio é 16x2 + 8x + 1 é (4x + 1)2, pois é a soma das raízes ao quadrado.
Veja alguns exemplos:
Exemplo 1:
Dado o trinômio m2 – m n + n2 , devemos tirar as raízes dos termos m2 e n2 , as raízes serão m e n, o dobro dessas raízes será 2. m . n que é diferente do termo m n (termos do meio), então esse trinômio não é quadrado perfeito.
Exemplo 2:
Dado o trinômio 4x2 – 8xy + y2, devemos tirar as raízes dos termos 4x2 e y2 , as raízes serão respectivamente 2x e y. O dobro dessas raízes deve ser 2 . 2x . y = 4xy, que é diferente do termo 8xy, então esse trinômio não poderá ser fatorado utilizando o quadrado perfeito.
Exemplo 3:
Dado o trinômio 1 + 9a2 – 6a.
Devemos, antes de usar as regras do quadrado perfeito, colocar o trinômio em ordem crescente de expoentes, ficando assim:
9a2 – 6a + 1.
Agora, tiramos a raiz dos termos 9a2 e 1, que serão respectivamente 3a e 1. O dobro dessas raízes será 2 . 3a . 1 = 6a, que é igual ao termo do meio (6a), então concluímos que o trinômio é quadrado perfeito e a forma fatorada dele é (3a – 1)2.
Por Danielle de Miranda
Graduada em Metemática