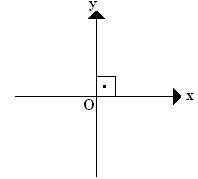
Se duas retas se cruzam e formam um ângulo de 90º elas são perpendiculares. A perpendicularidade dessas duas retas forma um sistema cartesiano ortogonal.
As duas retas são chamadas de eixos:
Eixo das abscissas: reta x.
Eixo das coordenadas: reta y.
Onde as retas x e y se encontram é formado um ponto, que é chamado de ponto de origem.
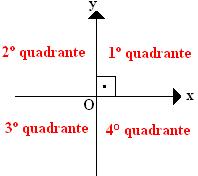
O sistema cartesiano ortogonal é dividido em quatro partes e cada uma é um quadrante.
Um ponto no sistema cartesiano ortogonal é formado por dois pontos, um do eixo das abscissas e outro do eixo das ordenadas.
O ponto no sistema cartesiano ortogonal é chamado de par ordenado.
.jpg)
O ponto X possui um número x que é a abscissa do ponto P.
O ponto Y possui um número y que é a ordenada do ponto P.
(x, y) é chamado de par ordenado do ponto P.
Portanto, para determinarmos um ponto P no sistema cartesiano ortogonal é preciso que as abscissas e as ordenadas sejam dadas.
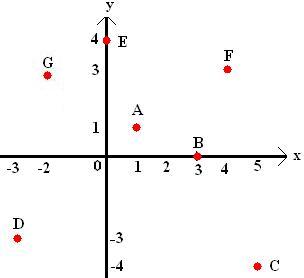
Veja o sistema cartesiano ortogonal abaixo e os pontos que estão indicados.
O ponto A (1, 1) encontra-se no 1° quadrante.
O ponto B (3, 0) encontra-se no eixo das abscissas x.
O ponto C (5, -4) encontra-se no 4º quadrante.
O ponto D (-3, -3) encontra-se no 3º quadrante.
O ponto E (0, 4) encontra-se no eixo das ordenadas
O ponto F (4, 3) encontra-se no 1º quadrante.
O ponto G (-2, 3) encontra-se no 2° quadrante.
Por Danielle de Miranda
Graduada em Matemática