O cálculo da probabilidade de eventos simultâneos determina a chance de dois eventos ocorrerem simultânea ou sucessivamente.
A fórmula para o cálculo dessa probabilidade decorre da fórmula da probabilidade condicional. Assim, teremos:
![]()
Se os eventos A e B forem independentes, ou seja, se o fato de ocorrer o evento B não alterar a probabilidade de ocorrer o evento A, a fórmula para o cálculo da probabilidade condicional será:
![]()
Vamos fazer alguns exemplos para explorar o uso da fórmula e a maneira correta de interpretar os problemas relacionados à probabilidade de eventos simultâneos.
Exemplo 1. Em dois lançamentos sucessivos de um mesmo dado, qual a probabilidade de ocorrer um número maior que 3 e o número 2?
Solução: perceba que a ocorrência de um evento não influencia a probabilidade de outro ocorrer, portanto são dois eventos independentes. Vamos distinguir os dois eventos:
A: sair um número maior que 3 → temos como possíveis resultados os números 4, 5 ou 6.
B: sair o número 2
Vamos calcular a probabilidade de ocorrência de cada um dos eventos. Observe que no lançamento de um dado, temos 6 valores possíveis. Assim:
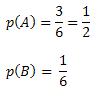
Dessa forma, teremos:
![]()
Exemplo 2. Numa urna há 30 bolinhas numeradas de 1 a 30. Serão retiradas dessa urna duas bolinhas, ao acaso, uma após a outra, sem reposição. Qual a probabilidade de sair um múltiplo de 10 na primeira e um número ímpar na segunda?
Solução: o fato de a retirada das bolinhas ocorrer sem reposição, implica que a ocorrência do primeiro evento interfere na probabilidade do segundo ocorrer. Portanto, esses eventos não são independentes. Vamos determinar cada um dos eventos.
A: sair um múltiplo de 10 → {10, 20, 30}
B: sair um número ímpar → {1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29}
A probabilidade de ocorrer os dois eventos sucessivamente será dada por:
![]()
Faremos os cálculos separadamente:
![]()
Para o cálculo de p(B|A) é preciso notar que não teremos mais 30 bolinhas na urna, pois uma foi retirada e não houve reposição, restando 29 bolinhas na urna. Assim,
![]()
Logo,
![]()
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática
Equipe Brasil Escola