Menor complementar é um determinante tirado de uma matriz quadrada, sendo que para calculá-lo é preciso eliminar uma linha e uma coluna da matriz, portanto, podemos concluir que cada elemento de uma matriz quadrada possui um menor complementar.
Por exemplo:
Dada a matriz quadrada A = 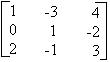
A = 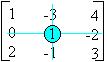
a 22 = = 1 . 3 – 2 . 4 = 3 – 8 = -5
Portanto, o menor complementar de a22 é -5.
A quantidade de elementos de uma matriz quadrada está diretamente ligada à quantidade de menor complementar que ela irá possuir, ou seja, se uma matriz possui 9 elementos, ela terá 9 menor complementar.
Levando em consideração a matriz A, o menor complementar do elemento a31 será:
A =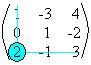
a 31 = = - 3 . (-2) – 1 . 4 = 6 – 4 = 2
Por Danielle de Miranda
Graduada em Matemática