O que são redes? Um conjunto de pontos interligados. Assim podemos definir rede, de uma maneira muito breve, segundo seu aspecto formal aparente. Rede é um agrupamento de pontos que se ligam a outros pontos por meio de linhas (MARTINHO; 2003).
Como exemplos de redes, temos:
● Redes sociais: os pontos são indivíduos e as linhas são interações sociais entre eles.
● Redes genéticas: as proteínas e genes são os pontos e as linhas são reações químicas.
● World Wide Web (WWW): os nodos (pontos) são os documentos HTML cujas conexões (linhas) são apontadores de uma página à outra.
● Redes neuronais: os pontos são neurônios conectados por axônios.
● As sociedades: os pontos são pessoas unidas por amizades, laços familiares e profissionais.
● Redes alimentares, ecossistemas.
● Redes de energia elétrica e os sistemas de transporte.
A arquitetura de uma rede não é suficiente para explicá-la ou caracterizá-la como um sistema com propriedades e um modo de funcionamento específico. Não basta identificarmos as ligações, as conexões. As questões importantes são, entre outras: “Como estão ligados os pontos na rede?”, “Para que servem tais ligações?”, “Como os pontos funcionam de forma interligada?” e “De que maneira esse conjunto de pontos e linhas opera como conjunto?”. Em suma, queremos saber quais as propriedades e as dinâmicas produzidas por um sistema desse tipo.
Fritjof Capra, no seu livro “A Teia da Vida” (CAPRA; 2004), cita algumas dessas propriedades:
“A primeira e mais óbvia propriedade de qualquer rede é a sua não-linearidade – ela se estende em todas as direções. Desse modo, as relações num padrão de rede são relações não-lineares. Em particular, uma influência, ou mensagem, pode viajar ao longo de um caminho cíclico, que poderá se tornar um laço de realimentação. (...) Devido ao fato de que as redes de comunicação podem gerar laços de realimentação, elas podem adquirir a capacidade de regular a si mesmas. Por exemplo, uma comunidade que mantém uma rede ativa de comunicação aprenderá com seus erros, pois as conseqüências de um erro se espalharão por toda a rede e retornarão para a fonte ao longo de laços de realimentação. Desse modo, a comunidade pode corrigir seus erros, regular a si mesma e organizar a si mesma. Realmente, a auto-organização emergiu talvez como a concepção central da visão sistêmica da vida, e, assim como as concepções de realimentação e auto-regulação, está estreitamente ligada a redes.”

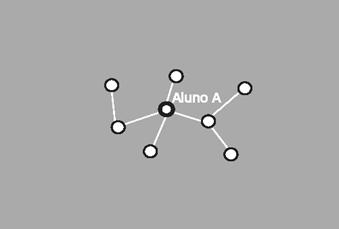
As linhas são mais importantes do que os pontos num desenho de rede. Isso porque são as conexões que fazem a rede. É o relacionamento entre os pontos que dá qualidade de rede ao conjunto. Não se tem um diagrama de redes só com pontos, mas, com efeito, pode-se perfeitamente desenhar uma rede só com linhas (Figura 4): os pontos aparecem no entrecruzamento das linhas. São as conexões (as linhas) que dão ao conjunto organicidade. E é o fenômeno de produção dessas conexões - a conectividade - que constitui a dinâmica de rede. A rede se exerce por meio da realização contínua das conexões; ela só pode existir na medida em que houver ligações sendo estabelecidas.
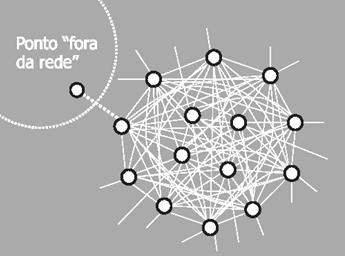
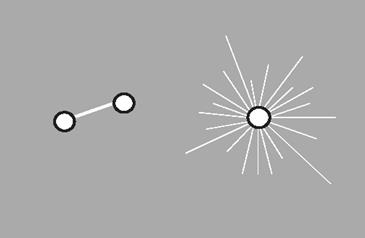
Cada conexão representa sempre um par de pontos, pois uma ligação só pode se estabelecer na medida da existência de dois elementos a serem ligados. Nesse sentido, uma linha vale por dois pontos. Em compensação, cada ponto pode manter uma infinidade de linhas que se projetam dele; pode possuir tantas linhas quantos forem os demais pontos pertencentes à rede a que ele estiver ligado:
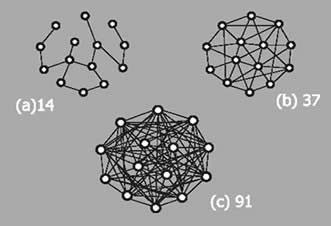
Outra propriedade a ser analisada, é a sua densidade. Quanto mais conexões (linhas) existir numa rede, mais densa ela será. Na figura, um mesmo conjunto de 14 pontos é apresentado com densidades diferentes. No diagrama "a", os 14 pontos estão interligados por 14 linhas; no diagrama "b", representando uma rede de densidade maior, 37 linhas entretecem os 14 pontos; e, no diagrama "c", os mesmos 14 pontos ligam-se por meio de 91 conexões – o que configura uma rede de alta densidade.
Assim, percebemos quase que de imediato que a densidade da rede não está relacionada diretamente ao número de pontos que a constituem, mas à quantidade de conexões que esses pontos estabelecem entre si. Esse é o aspecto mais importante e parece provar que a capacidade da rede ultrapassa em muito a mera soma de seus elementos. Podemos perceber, ainda, outro aspecto da densidade: o limite máximo de conectividade do sistema é alcançado quando todos os pontos estabelecem ligações com os demais; quando todos estão ligados com todos diretamente, sem qualquer ponto intermediário. Calcular, portanto, a densidade da rede pode proporcionar um bom indicador da sua "capacidade produtiva" num determinado momento. Assim, percebemos que para determinarmos a máxima densidade de uma rede, operamos da seguinte forma:
dMAX = nr. de pontos x (nr. de pontos – 1) / 2
No nosso exemplo, teríamos:
dMAX = nr. de pontos x (nr. de pontos – 1) / 2
dMAX = 14 x ( 14 – 1) / 2
dMAX = 14 x 13 / 2
dMAX = 182 / 2
dMAX = 91 conexões
Dizemos que o potencial de relacionamento desta rede, com 14 pontos, tem seu máximo grau de relações quando atingir 91 conexões. Ou seja, em uma turma com 14 alunos, estes podem produzir 91 relações, de um para um, diferentes entre si.
O cálculo da densidade demonstra claramente como uma maior quantidade de participantes pode produzir um grau novo de relações no âmbito de uma rede. Um grupo de três pessoas pode produzir somente três relacionamentos; porém, um grupo de quatro pessoas (um indivíduo a mais) pode produzir o dobro de interligações (seis). Um grupo uma vez maior (de seis pessoas) pode produzir, por sua vez, cinco vezes mais relacionamentos do que produz o grupo com três elementos.
Desta forma, a lição trazida pela densidade é de que quanto maior for o número de conexões, mais compacta, integrada, coesa e orgânica será a rede (MARTINHO; 2003)
Referências
CANCHO, R. F.; JANSEEN, C. e SOLÉ, R. V. Topology of technology graphs: Small world patterns in electronic circuits. The American Phisycal Society. Review E 64. 2001.
CAPRA, F. A teia da vida: uma nova compreensão científica dos sistemas vivos. São Paulo: Cultrix, 2004.
CASTELLS, Manuel. A sociedade em rede. São Paulo: Paz e Terra, 2000.
FERNÁNDEZ, P.; SOLÉ, R. V. The Role of Computation in Complex Regulatory Networks. In: SCALE-FREE NETWORKS AND GENOME BIOLOGY, 2003. Anais. Landes Bioscience, 2003.
JOHNSON, S. Emergência: a dinâmica de rede em formigas, cérebros, cidades e software. Rio de Janeiro: Jorge Zahar Editor, 2003.
MARTINHO, Cássio. Redes, uma introdução às dinâmicas da conectividade e da auto-organização (texto), WWF – Brasil, 2003.
WELLMAN, Barry. Structural Analysis: From Method and Metaphor to Theory and Substance. Publicado em: WELLMAN, Barry e BERKOWITZ, S. D. editores. Social Structures: A Network Approach. Cambridge: Cambridge University Press, 1988.
WILENSKY, U. NetLogo Small Worlds model. Disponível em Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL. 2005.
Por Wendley Souza
Prof. Engenharia da Computação