A transformação de Lorentz é um conjunto de equações que relacionam as coordenadas no espaço-tempo de um evento em altas velocidades. Essas equações foram cruciais para o físico Albert Einstein desenvolver a teoria da relatividade. Com elas, foi possível descrever o movimento de corpos em altíssimas velocidades, próximas à velocidade da luz (a velocidade máxima da física). Com isso, foi possível também obter curiosos fenômenos relativísticos, como a dilatação temporal e a contração do espaço.
Leia também: O que diz a teoria da relatividade?
Tópicos deste artigo
- 1 - Resumo sobre a transformação de Lorentz
- 2 - O que é a transformação de Lorentz?
- 3 - Consequências da transformação de Lorentz
- 4 - Transformação de Lorentz para a velocidade
- 5 - Einstein e a transformação de Lorentz
- 6 - Exercícios sobre transformação de Lorentz
Resumo sobre a transformação de Lorentz
- A transformação de Lorentz é um conjunto de equações que relacionam as coordenadas no espaço-tempo de um evento em altas velocidades.
- São fundamentais para a relatividade de Einstein.
- São escritas como: x' = γ · (x - v ⋅ t)
\(y' = y \\ z' = z \\ t' = \gamma \cdot \left(t - \frac{v \cdot x}{c^2}\right) \\\)
- O fator de Lorentz é dado por: \(\gamma = \frac{1}{\sqrt{1 - \left(\frac{v}{c}\right)^2}} \\ \)
- As consequências da transformação de Lorentz são a dilatação temporal e a contração da distância.
- No limite de baixas velocidades, as transformações de Lorentz recaem nas transformações de Galileu da mecânica clássica.
O que é a transformação de Lorentz?
A transformação de Lorentz é um conjunto de equações encontradas pelo físico neerlandês Hendrik Lorentz que foram fundamentais para o desenvolvimento da relatividade de Einstein. Sendo úteis para velocidades relativísticas, ou seja, próximas à da luz (c=299.792.458 m/s), as equações da transformação de Lorentz relacionam as coordenadas no espaço-tempo de um evento em dois referenciais inerciais, O e O'.
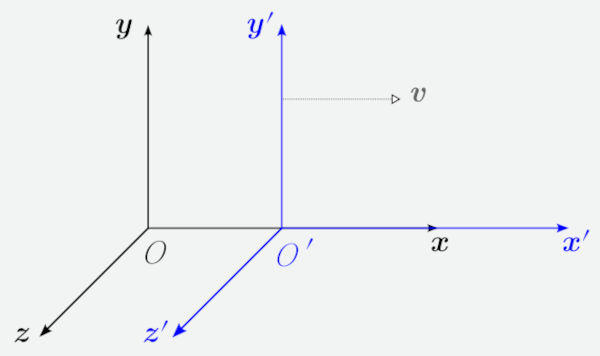
Se O' está se movendo em relação a O com velocidade v no sentido positivo dos eixos x e x', as relações entre as coordenadas nos dois referenciais são dadas pela transformação de Lorentz:
\(x' = \gamma \cdot (x - v \cdot t) \\ y' = y \\ z' = z \\ t' = \gamma \cdot \left(t - \frac{v \cdot x}{c^2}\right) \\ \)
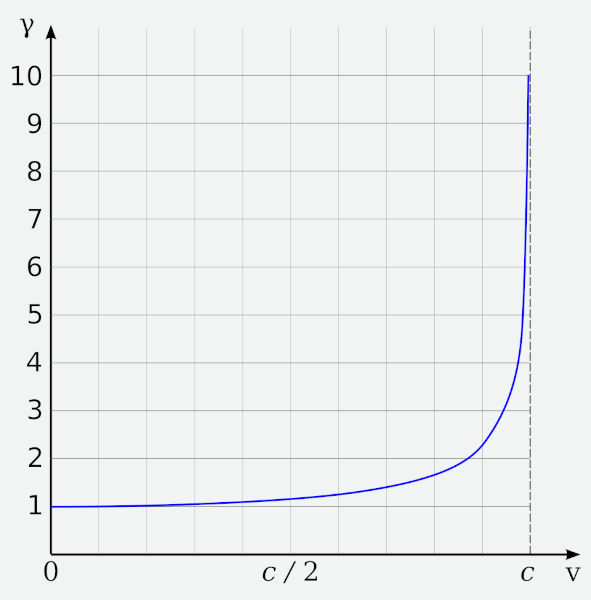
Vale destacar que \(\gamma = \frac{1}{\sqrt{1 - \left(\frac{v}{c}\right)^2}} \\ \) é o fator de Lorentz. O fator de Lorentz aumenta exponencialmente com o aumento da velocidade. Assim, conforme a velocidade se aproxima da velocidade da luz, o fator de Lorentz tende a crescer rapidamente, revelando os efeitos relativísticos:
Consequências da transformação de Lorentz
-
Dilatação do tempo
Um observador que está se movendo com velocidades próximas à da luz em relação a outro mede um intervalo de tempo maior. Assim, o relógio do observador em movimento atrasa em relação ao relógio do observador em repouso. Se o observador está se movendo com velocidade relativa v , o intervalo de tempo medido é:
\(\Delta t = \gamma \cdot \Delta t_0 \\ \)
Um experimento mental famoso desse fato é o paradoxo dos gêmeos. Um gêmeo viaja de foguete por um longo tempo em velocidades próximas à da luz, enquanto o outro gêmeo permanece na Terra vivendo normalmente.

Quando o gêmeo viajante retorna ao planeta, percebe que o seu irmão está muito mais velho que ele.

Isso ocorreu por causa da dilatação temporal que ele sofreu ao viajar em velocidades tão altas. Esse fenômeno pode ser medido com partículas altamente energéticas oriundas de raios cósmicos.
-
Contração da distância
Outro fenômeno que também acontece ao viajar em velocidades tão altas é o da contração dos objetos. Em velocidades próximas à da luz, o espaço ao redor do objeto é comprimido, fazendo-o diminuir consideravelmente de tamanho. Um observador que está se movendo com velocidades próximas à da luz em relação a outro mede um comprimento menor. Se o observador está se movendo com velocidade relativa v , o comprimento medido é:
\(L = \frac{L_0}{\gamma} \\ \)
Transformação de Lorentz para a velocidade
Se uma partícula está se movendo com velocidade u' no sentido positivo do eixo x' de um referencial inercial O' que está se movendo com velocidade v no sentido positivo do eixo x de um segundo referencial inercial O' , a velocidade u da partícula no referencial O é dada por:
\(u = \frac{u' + v}{1 + \frac{u' \cdot v}{c^2}} \\ \)
Einstein e a transformação de Lorentz
Antes de Einstein, os físicos tratavam a variável tempo como algo absoluto, invariável. Todas as descrições físicas da mecânica newtoniana eram calculadas com as transformações de Galileu, dadas por:
x' = x - v · t
y' = y
z' = z
t' = t
Em 1905, o físico teórico alemão Albert Einstein publicou o trabalho referente à teoria da relatividade restrita, na qual passou a tratar a velocidade da luz como uma entidade física absoluta, invariável, e não mais o tempo. No lugar das transformações de Galileu, ele passou a usar as transformações de Lorentz, revolucionando toda a física.
As transformações de Galileu ainda são válidas para baixas velocidades (comparadas com a velocidade da luz) — inclusive, em um limite de baixas velocidades, as transformações de Lorentz recaem nas transformações de Galileu.
Leia também: O que é o espaço-tempo?
Exercícios sobre transformação de Lorentz
Questão 1
A sonda Parker Solar Probe, da Nasa, é o objeto macroscópico mais rápido já criado pelo ser humano, atingindo a incrível velocidade de 635.266 km/h. Apesar de ser uma velocidade pequena comparada à velocidade da luz, os fenômenos relativísticos começam a aparecer de forma sutil, imperceptíveis para o ser humano, mas mensuráveis. Calcule a diferença na passagem do tempo causada pelo fenômeno da dilatação temporal da nave em comparação com o planeta Terra em um dia completo.
A) 0,015 s
B) 0,5 s
C) 1 s
D) 1,5 s
E) 3,5 s
Resolução:
Alternativa A.
Primeiro façamos a transformação da unidade de medida:
635.266 km/h = 176462,778 m/s
Então, o fator de Lorentz será:
\(\gamma = \frac{1}{\sqrt{1 - \left(\frac{v}{c}\right)^2}} \\ \gamma = \frac{1}{\sqrt{1 - \left(\frac{176462{,}778}{299792458}\right)^2}} \\ \gamma = \frac{1}{\sqrt{1 - (0{,}00058861646)^2}} \\ \gamma = \frac{1}{\sqrt{1 - 0{,}000000346469337}} \\ \gamma = \frac{1}{\sqrt{0{,}99999965353}} \\ \gamma = \frac{1}{0{,}99999982676} \\ \gamma = 1{,}00000017324 \\ \)
Um dia completo tem 86400 s, então usando a fórmula da dilatação temporal:
\(\Delta t = \gamma \cdot \Delta t_0 \\ \Delta t = 1{,}00000017324 \cdot 86400 \\ \Delta t = 86400{,}0149679\ \text{s} \\ \)
Assim, em um dia completo, há uma diferença de 0,015 s na passagem do tempo da nave com relação à Terra.
Questão 2
A sonda Parker do exercício anterior, em repouso, tem uma altura de 3 m. Encontre o quanto a nave diminuiu de altura devido ao fenômeno da contração da distância quando atingiu a velocidade de 635.266 km/h.
A) 1 pm
B) 2,35 nm
C) 0,5 μm
D) 3,46 cm
E) 1 m
Resolução:
Alternativa C.
Usando a fórmula da contração da distância:
\(L = \frac{L_0}{\gamma} \\ L = \frac{3}{1{,}00000017324} \\ L = 2{,}99999948028\ \text{m} \\ \)
Assim, a nave diminuiu cerca de 0,5 μm.
Fontes
CARRON, Wilson; GUIMARÃES, Osvaldo. As faces da física (vol. único). 1. ed. Moderna, 1997.
HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos da Física: Óptica e Física Moderna (vol. 4). 9 ed. Rio de Janeiro, RJ: LTC, 2012.
NUSSENZVEIG, Herch Moysés. Curso de física básica: Óptica, Relatividade e Física Quântica (vol. 4). 2 ed. São Paulo: Editora Blucher, 2014.

