Para entender o potencial elétrico de uma esfera condutora eletrizada devemos analisar primeiramente o que ocorre dentro da esfera, que ao ser eletrizada alcança rapidamente o equilíbrio eletrostático em razão do espalhamento uniforme das cargas excedentes através de sua superfície externa. Nessa situação, o campo elétrico e a força elétrica dentro dessa esfera são nulos.
Não pare agora... Tem mais depois da publicidade ;)
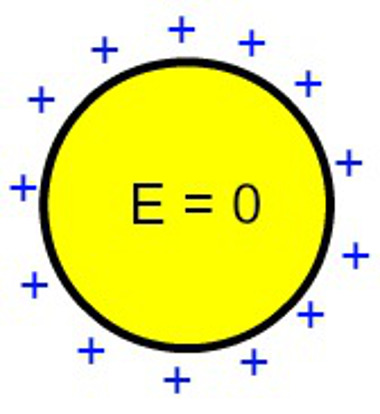
O campo elétrico (E) no interior da esfera eletrizada é nulo
Assim, se colocarmos uma partícula eletrizada com carga q sobre um ponto A dentro da esfera e ela for deslocada para um ponto B, também interno à esfera, nenhum trabalho (τ) será realizado sobre ela e pela equação: VA – VB = τ/q, temos que VA = VB, se VA fosse diferente de VB haveria fluxo de cargas entre esses dois pontos, e isso não pode ocorrer quando a esfera está em equilíbrio eletrostático, dessa forma, podemos dizer que:
No interior de uma esfera eletrizada em equilíbrio eletrostático, todos os pontos têm o mesmo potencial elétrico.
Quando temos um ponto S exatamente na superfície da esfera ocorre novamente que o trabalho realizado para levar uma carga q de A ou B até S é igual a zero, dessa forma podemos concluir que:
O potencial elétrico em qualquer ponto situado no interior de uma esfera eletrizada em equilíbrio eletrostático é igual ao potencial em sua superfície.
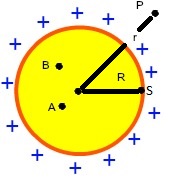
A esfera pode ser considerada como uma carga puntiforme
Agora temos que saber qual é o valor do potencial elétrico na superfície da esfera em equilíbrio eletrostático, e para isso devemos lembrar que esferas eletrizadas nessas condições de equilíbrio eletrostático podem ser consideradas como se tivessem toda sua carga concentrada em seu centro, então se tivermos uma esfera de raio R, o potencial em sua superfície será dado por V = KoQ/R, e também se tivermos um ponto P localizado externamente à esfera a uma distância r do seu centro (dessa forma r > R), o potencial elétrico da esfera em P pode ser calculado pela equação (veja a figura acima):
V = KoQ/r
O potencial para pontos no interior da esfera (r ≤ R) é constante, e para pontos fora da esfera (r > R) decresce de forma inversamente proporcional à distância (r).
Por Paulo Silva
Graduado em Física
