Intensidade de Energia Transmitida pelo Som
Física
No dia a dia é muito comum ver as pessoas falando que o som emitido por um aparelho de rádio ligado no volume máximo tem grande intensidade ou que o aparelho tem um “som forte”, ouve-se dizer também que o som emitido por um relógio é de baixa intensidade ou no linguajar popular o “som é fraco”.
Além da velocidade, do comprimento e da frequência, a onda sonora possui outra importante propriedade que é a intensidade. Essa propriedade está relacionada com a energia de vibração da fonte emissora. Quando uma onda sonora se propaga, ela transmite energia que propaga em todas as direções. A intensidade sonora será cada vez maior quanto maior for a energia que a onda sonora estiver transportando.
A intensidade de energia sonora pode ser medida através do quociente entre a potência, também conhecida como taxa média, e a área, matematicamente:
I = P/A (1)
Onde P pode ser calculado como sendo a razão entre a energia transmitida e o intervalo de tempo, veja:
P = ΔE/Δt (2)
Substituindo a equação (2) na equação (1), temos que a intensidade sonora pode ser calculada a partir da seguinte expressão matemática:
I = ΔE/ A.Δt
A unidade de intensidade no Sistema Internacional de Unidades (SI) é o watt por metro quadrado (W/m2).
Por Marco Aurélio da Silva
Equipe Brasil Escola
Ondas - Física - Brasil Escola
Gostaria de fazer a referência deste texto em um trabalho escolar ou acadêmico? Veja:
SANTOS, Marco Aurélio da Silva. "Intensidade de Energia Transmitida pelo Som"; Brasil Escola. Disponível em: https://brasilescola.uol.com.br/fisica/intensidade-energia-transmitida-pelo-som.htm. Acesso em 19 de outubro de 2021.
(UEL-PR) (adaptada) A poluição sonora em grandes cidades é um problema de saúde pública. A classificação do som como forte ou fraco está relacionada ao nível de intensidade sonora I, medido em watt/m2. A menor intensidade audível, ou limiar de audibilidade, possui intensidade I0 = 10–12 watt/m2, para a frequência de 1000 Hz. A relação entre as intensidades sonoras permite calcular o nível sonoro, NS, do ambiente, em decibéis (dB). A tabela a seguir mostra a relação do nível sonoro com o tempo máximo de exposição a ruídos.
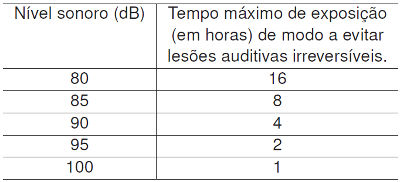
Com base nessa tabela, no texto e supondo que o ruído em uma avenida com trânsito congestionado tenha intensidade de 10–3 watt/m2, considere as afirmativas a seguir.
I. O nível sonoro para um ruído dessa intensidade é de 90 dB.
II. O tempo máximo em horas de exposição a esse ruído, a fim de evitar lesões auditivas irreversíveis, é de 4 horas.
III. Se a intensidade sonora considerada for igual ao limiar de audibilidade, então o nível sonoro é de 1 dB.
IV. Sons de intensidade de 1 watt/m2 correspondem ao nível sonoro de 100 dB.
Assinale a alternativa correta.
a) Somente as afirmativas I e II são corretas.
b) Somente as afirmativas I e IV são corretas.
c) Somente as afirmativas III e IV são corretas.
d) Somente as afirmativas I, II e III são corretas.
e) Somente as afirmativas II, III e IV são corretas.
(UFT-TO) Um som é produzido por um alto-falante ao ar livre, que se situa sobre uma superfície plana. As ondas sonoras produzidas por esse alto-falante atingem uma pressão máxima de 84 [Pa] a 10 [m] do alto-falante. Supondo que a intensidade das ondas sonoras seja igual em todas as direções na área de superfície do hemisfério, qual é a potência acústica do som emitido pelo alto-falante?
Considere a intensidade das ondas sonoras dada por:
Em que:
PMAX= Pressão máxima da onda sonora [Pa]
ρ = Densidade do ar = 1,20 [kg/m3]
v = Velocidade do som no ar ≅ 350 [m/s]
a) 1000 W
b) 1,68π kW
c) 4,12π kW
d) 13 kW
e) 13 MW
Mais Questões
Proibida a reprodução total ou parcial sem prévia autorização (Inciso I do Artigo 29 Lei 9.610/98)