Nos estudos de termodinâmica vimos que dilatação térmica nada mais é do que o aumento das dimensões de um corpo quando há aumento de temperatura. Podemos dizer que isso ocorre com quase todos os materiais no estado sólido, líquido ou gasoso. Com base na dilatação linear, em que podemos calcular o aumento de tamanho de um corpo em uma única dimensão, veremos como calcular a dilatação superficial, ou seja, o aumento de sua área superficial quando o corpo é aquecido.
Dilatação superficial dos sólidos
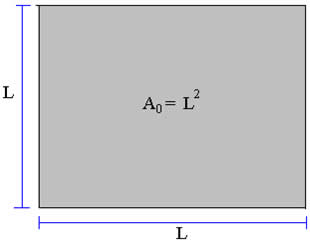
Vamos considerar uma chapa metálica (figura acima) cujas dimensões, na temperatura T0, são: largura L0 e altura L0. Dessa forma, sua área é: A0 = L02. Agora, se aquecermos essa chapa a uma temperatura T, maior do que a temperatura inicial, veremos que a chapa se dilatará passando a ter uma área maior (A) do que a área inicial, conforme a figura abaixo.
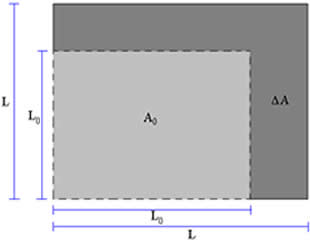
De acordo com a figura acima vemos que a chapa metálica, após ser aquecida, teve suas dimensões aumentadas, ou seja, houve aumento de sua área. A fim de calcular o aumento da área (ΔA = A – A0), quando a chapa metálica é submetida a uma variação de temperatura (ΔT = T – T0), utilizamos uma equação semelhante à equação que fornece a dilatação linear, portanto temos:
ΔA= A0 .β .ΔT ou A=A0 (1+ β . ΔT)
Onde A0 é a área inicial da chapa, β é o coeficiente de dilatação superficial da chapa e ΔT é a variação de temperatura da chapa metálica. Temos que lembrar que β = 2.α. No SI as unidades são m², K-1 e K. É importante lembrar que, apesar de Kelvin ser a unidade do SI adotada, é mais usual o °C-1 e o °C.
Por Domiciano Marques
Graduado em Física