PUBLICIDADE
Ao estudarmos o movimento de uma carga elétrica imersa em um campo magnético uniforme, perceberemos que a trajetória descrita por ela dependerá do ângulo formado entre a velocidade da partícula e o campo magnético onde ela está imersa. A fim de termos um melhor aproveitamento do estudo do comportamento da partícula no campo uniforme, vamos dividir nossa análise em três casos distintos.
Primeiro caso: θ = 0º ou θ = 180º
O caso θ = 0º ocorre quando a velocidade tem o mesmo sentido de 
. Já o caso θ = 180º ocorre quando a velocidade tem sentido oposto ao de . Sabemos que o módulo da força magnética é dado por:
F= |q|.v .B .senθ
Como sen 0º = sen 180º = 0, temos que:
- nos dois casos a força magnética é nula. De tal modo, se não houver outras forças atuando na partícula, a aceleração será nula, e teremos então um movimento retilíneo e uniforme.
Segundo caso: θ = 90º
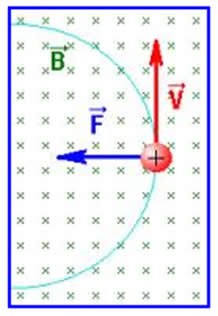
Quando θ = 90º, os vetores
são perpendiculares entre si. Nesse caso, o módulo da força magnética é dado por:
F= |q|.v .B .senθ,
como sen 90°=1,temos:
F= |q|.v .B
Nesse caso, sabemos que a força sempre é perpendicular ao vetor velocidade. Ela não altera o módulo da velocidade, mas apenas a direção da velocidade. Dessa forma, ocorre um movimento circular uniforme. Como a partícula descreve um movimento circular uniforme, temos a possibilidade de determinar o valor do raio da trajetória percorrida pela partícula através da seguinte equação:
A partir do raio da trajetória descrita pela partícula, podemos calcular o período T do movimento no intervalo de tempo de 1 volta. A equação que nos permite fazer o cálculo é a seguinte:
Terceiro caso: θ ≠0°, θ ≠90°, θ ≠180°,
Ou seja, q é lançada obliquamente à direção do campo. Nesse caso, decompõe-se a velocidade 
em dois componentes:
- componente vx, na direção : causa um MRU
- componente vy, perpendicular a : causa um MCU
Portanto, a simultaneidade desses dois movimentos produz um movimento helicoidal uniforme.
Por Domiciano Marques
Graduado em Física
Equipe Brasil Escola
