A conversão de medidas é uma operação que fazemos para alterar a dimensão de uma determinada medida, tornando-a apropriada para o sistema de análise que está sendo utilizado. Toda unidade é múltipla ou submúltipla de outra unidade, sendo, portanto, necessário conhecer apenas o fator de conversão para transformar o valor de uma unidade no valor de outra unidade.
A conversão de medidas é importante para a compreensão de diversos fenômenos matemáticos, físicos, químicos e biológicos, por exemplo, pois, às vezes, uma determinada unidade pode não ser adequada para expressar o valor ao sistema estudado. Uma forma interessante de padronização das unidades se dá pela adoção do Sistema Internacional de Unidades, o SI.
Leia também: Como transformar um número em notação científica?
Tópicos deste artigo
- 1 - Resumo sobre conversão de medidas
- 2 - Videoaula sobre conversão de medidas
- 3 - Conversão de medidas de comprimento, massa e volume
- 4 - Conversão de medidas de comprimento
- 5 - Conversão de medidas de massa
- 6 - Conversão de medidas de volume
- 7 - Conversão de medidas de tempo
- 8 - Conversão de medidas de área
- 9 - Conversão de medidas de temperatura
- 10 - Conversão de medidas de velocidade
- 11 - Sistema internacional de unidades
- 12 - Exercícios resolvidos sobre conversão de medidas
Resumo sobre conversão de medidas
- A conversão de medidas é uma operação essencial para alteração da dimensão de uma determinada unidade de medida.
- Para converter medidas, é necessário conhecer apenas o fator de conversão para transformar os valores.
- Toda unidade de medida é múltipla ou submúltipla de outra unidade pertencente ao mesmo universo.
- A conversão de medidas de comprimento, massa e volume pode ser feita por meio de multiplicações ou divisões sucessivas em bases de 10.
- Podemos converter as medidas de temperatura, Celsius (°C) e Fahrenheit (°F), usando fórmulas específicas. Cada 1 °C corresponde a 1,8 °F.
- Para medidas de tempo, os submúltiplos do segundo são alcançados por meio de operações com base de 10, e seus múltiplos, por operações com base de 60.
- A conversão de múltiplos e submúltiplos de área, em termos de m2, ocorre em bases de 100 (ou seja, 102).
- Para converter o litro e seus múltiplos e submúltiplos, usamos a base de 10.
- Para medidas volumétricas em metros cúbicos, a conversão é feita pela multiplicação ou divisão por 1000 (103).
- Para medidas de velocidade, deve-se converter, ao mesmo tempo, a unidade de comprimento e a unidade de tempo.
- Para se converter um valor de km/h para m/s, dividimos o valor da velocidade por 3,6.
- Ao se converter uma unidade, busca-se fazer uma melhor adaptação do valor ao sistema de estudo.
Videoaula sobre conversão de medidas
Conversão de medidas de comprimento, massa e volume
As unidades de comprimento, massa e volume apresentam uma unidade fundamental, sendo metro (m) para o comprimento, grama (g) para a massa e litro (L) para o volume. Essas unidades fundamentais podem ser convertidas para unidades múltiplas ou submúltiplas, as quais são identificadas pelos seguintes prefixos:
|
Prefixo |
Representado por |
O que significa |
|
quilo- |
k |
Um milhar da unidade fundamental, ou seja, 1000 vezes maior que a unidade fundamental. |
|
hecto- |
h |
Uma centena da unidade fundamental, ou seja, 100 vezes maior que a unidade fundamental. |
|
deca- |
da |
Uma dezena da unidade fundamental, ou seja, 10 vezes maior que a unidade fundamental. |
|
deci- |
d |
Um décimo da unidade fundamental, ou seja, 10 vezes menor que a unidade fundamental. |
|
centi- |
c |
Um centésimo da unidade fundamental, ou seja, 100 vezes menor que a unidade fundamental. |
|
mili- |
m |
Um milésimo da unidade fundamental, ou seja, 1000 vezes menor que a unidade fundamental. |
Quando desejamos alcançar múltiplos ou submúltiplos sucessivos, devemos fazer multiplicações ou divisões sucessivas por 10 (bases de 10), conforme é ilustrado na figura a seguir:

Perceba, portanto, que para alcançar um valor em milímetro (mm) a partir do metro (m), necessita-se de três multiplicações sucessivas por 10, ou seja, 10 x 10 x 10, o que é igual a 1000. Da mesma forma, se desejamos um valor em grama (g), a partir de centigrama (cg), é necessário realizar duas divisões sucessivas por 10, ou seja, dividir por 10 e, depois, por 10 novamente, o que é igual a dividir por 100.
Conversão de medidas de comprimento
As unidades de comprimento são referentes ao sistema métrico, no qual a unidade “metro”, representada pela letra “m”, é considerada a unidade fundamental. A partir dela, são estabelecidos múltiplos e submúltiplos que são alcançados pela multiplicação ou divisão em bases de 10.
Observe os valores na tabela:
|
Unidade fundamental |
Unidade |
Símbolo |
Conversão |
|
1 metro (m) |
quilômetro |
km |
1 km = 1000 m |
|
hectômetro |
hm |
1 hm = 100 m |
|
|
decâmetro |
dam |
1 dam = 10 m |
|
|
decímetro |
dm |
1 dm = 0,1 m |
|
|
centímetro |
cm |
1 cm = 0,01 m |
|
|
milímetro |
mm |
1 mm = 0,001 m |
Vejamos, a seguir, alguns exemplos clássicos.
Exemplo 1:
- Como converter 2 quilômetros em metros:
Podemos realizar essa conversão de duas formas:
Em primeiro lugar, ao observarmos os valores da tabela acima, percebemos que 1 quilômetro (km) equivale a 1000 metros (m). Portanto, 2 km são:
2 x 1000 m = 2000 m
Isto é, 2 km equivalem a 2000 metros.
De uma segunda forma, podemos fazer a conversão por multiplicações sucessivas. Na imagem abaixo, observe que entre o quilômetro e o metro existem duas unidades: hectômetro e decâmetro:

Assim, de quilômetro para metro, devemos realizar 3 multiplicações sucessivas por 10 (quilômetro para hectômetro; hectômetro para decâmetro; e decâmetro para metro), ou seja, vamos multiplicar:
2 x 10 x 10 x 10 = 2000 m
Ou seja, o resultado é 2000 metros.
Exemplo 2:
- Como converter 10 centímetros em decâmetros:
Também é possível realizar essa conversão de duas formas. Em primeiro lugar, tomando a tabela de unidades de comprimento como auxílio, vimos que 1 decâmetro (dam) equivale a 10 metros. Proporcionalmente, percebemos que 1 m equivale a 0,1 dam, conforme é demonstrado a seguir:
1 dam -------------- 10 m
x dam -------------- 1 m
x = 1/10 = 0,1 dam
Ainda na tabela, veja que 1 centímetro (cm) equivale a 0,01 m. Proporcionalmente, perceba que 10 cm é igual a 0,1 m.
Assim, podemos pensar que:
10 cm = 0,1 m
0,1 m = 0,1 x 1 m
0,1 x 1 m = 0,1 x 0,1 dam
Ou seja,
10 cm = 0,01 dam.
Também podemos fazer a conversão via divisões sucessivas. Observe, na imagem abaixo, que entre centímetro e decâmetro temos duas unidades (decímetro e metro):

Portanto, o valor em centímetro é alcançado por meio de três divisões sucessivas por 10 (centímetro para decímetro; decímetro para metro; e metro para decâmetro). Ou seja: 10 cm = 10/1000 dam, que é igual a 0,01 dam.
→ Conversão de outras medidas de comprimento
Em áreas científicas, como Física, Química e Biologia, é comum o uso de unidades de medidas ainda menores que o metro, uma vez que a dimensão dos sistemas, por vezes, está em nível microscópico ou atômico. Para isso, temos, por exemplo, as unidades micrômetro, nanômetro e angström.
- 1 micrômetro (µm) = 0,000001 m (10−6 m, ou seja, 1 milionésimo de metro)
- 1 nanômetro (nm) = 0,000000001 m (10−9 m, ou seja, 1 bilionésimo de metro)
- 1 angström (Å) = 0,0000000001 m (10−10 m)
Fora do nosso sistema convencional, temos as unidades do sistema imperial de comprimento, no qual se encontram as unidades pés, polegadas, jardas e milhas.
- 1 pé = 0,3048 m
- 1 polegada = 0,0254 m
- 1 jarda = 0,9144 m
- 1 milha = 1609,34 m
Veja também: Qual a relação entre medidas de capacidade e medidas de volume?
Conversão de medidas de massa
As unidades de massa possuem como ponto de partida, ou seja, como unidade fundamental, o grama, representado pela letra “g”. As conversões em múltiplos e submúltiplos também seguem operações com bases de 10, assim como o sistema métrico.
Observe os valores na tabela:
|
Unidade fundamental |
Unidade |
Símbolo |
Conversão |
|
1 grama (g) |
quilograma |
kg |
1 kg = 1000 g |
|
hectograma |
hg |
1 hg = 100 g |
|
|
decagrama |
dag |
1 dag = 10 g |
|
|
decigrama |
dg |
1 dg = 0,1 g |
|
|
centigrama |
cg |
1 cg = 0,01 g |
|
|
miligrama |
mg |
1 mg = 0,001 g |
Vejamos alguns exemplos para fixação.
Exemplo 1:
- Como converter 35 hectogramas em miligramas:
Há duas formas de fazer a conversão. Em primeiro lugar, podemos verificar a tabela de medidas e ver que 1 hectograma (ou 1 hg) equivale a 100 gramas (nossa unidade fundamental). Dessa forma, é possível entender que 35 hg equivalem a 35 x 100 gramas, ou seja, 3500 gramas.
Também verificamos na tabela que 1 miligrama (ou 1 mg) equivale a 0,001 grama. Proporcionalmente, então, entende-se que 1 grama é igual a 1000 miligramas, como mostra o cálculo a seguir:
1 mg -------------- 0,001 g
x mg -------------- 1 g
x = 1/0,001 = 1000 mg
Assim, pensemos:
35 hg = 3500 g
3500 g = 3500 x 1 g
3500 x 1 g = 3500 x 1000 mg
Ou seja,
35 hg = 3500000 mg.
Também é possível fazer a conversão por meio das operações sucessivas, neste caso, fazendo o seguinte caminho de multiplicações sucessivas: de hg para dag; de dag para g; de g para dg; de dg para cg; e, por fim, de cg para mg.
Observe:
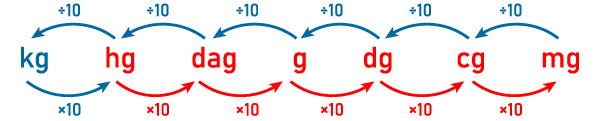
São cinco multiplicações sucessivas por 10, ou seja, vamos multiplicar o valor em hg por 100000 para alcançar o correspondente em mg. Portanto, temos:
35 x 100000 = 3500000 mg
Exemplo 2:
- Como converter 23 centigramas em decigramas:
Como vimos anteriormente, há duas formas de se fazer essa conversão.
Em primeiro lugar, observando a tabela, verificamos que 1 centigrama (cg) é igual a 0,01 grama (g). Portanto, podemos dizer que 23 cg é igual a 23 x 0,01 g, que é igual a 0,23 g.
Vimos, também, que 1 dg é equivalente a 0,1 g. Portanto, proporcionalmente, 1 g é igual a 10 dg, conforme mostra o cálculo a seguir:
1 dg -------------- 0,1 g
x dg -------------- 1 g
x = 1/0,1 = 10 dg
Assim, seguimos a sequência:
23 cg = 0,23 g
0,23 g = 0,23 x 1 g
0,23 x 1 g = 0,23 x 10 dg
Ou seja,
23 cg = 2,3 dg.
Realizando a conversão por meio de operações sucessivas, podemos afirmar que decigrama é a primeira unidade acima de centigrama.

Dessa forma, uma simples divisão por 10 converte o valor de cg para dg. Ou seja, dividimos 23/10 e chegamos a 2,3 dg.
→ Conversão de outras medidas de massa
Há também a unidade de massa tonelada (t ou ton), cuja conversão é feita da seguinte forma:
- 1 tonelada (t) = 1000000 g (1 milhão de gramas)
Nas áreas científicas, também é comum o uso da unidade micrograma em trabalhos da área de Química, Física e Biologia. Dessa forma:
- 1 micrograma (µg) = 0,000001 g (10−6 g, ou seja, 1 milionésimo de grama)
O sistema imperial também apresenta as seguintes unidades de massa:
- 1 grão = 0,0648 g
- 1 onça = 28,3495 g
- 1 libra = 453,592 g
- 1 pedra = 6350,29 g
- 1 tonelada imperial = 1,016 x 106 g
Conversão de medidas de volume
Existem dois tipos de unidades volumétricas, uma tem o litro (símbolo L ou l) como unidade fundamental e a outra, o sistema cúbico, que é derivado do sistema de unidades de comprimento. As conversões entre o litro e seus múltiplos e submúltiplos utiliza a base de 10, assim sendo:
|
Unidade fundamental |
Unidade |
Símbolo |
Conversão |
|
1 litro (L) |
quilolitro |
kL |
1 kL = 1000 L |
|
hectolitro |
hL |
1 hL = 100 L |
|
|
decalitro |
daL |
1 daL = 10 L |
|
|
decilitro |
dL |
1 dL = 0,1 L |
|
|
centilitro |
cL |
1 cL = 0,01 L |
|
|
mililitro |
mL |
1 mL = 0,001 L |
Vejamos um exemplo de conversão.
Exemplo 1:
- Como converter 365 mililitros em decilitros:
Cada 1 mL equivale a 0,001 L. Portanto, 365 mL equivalem a 365 x 0,001 L, ou seja, 0,365 L.
Da mesma forma, 1 dL equivale a 0,1 L, portanto, proporcionalmente, 1 L equivale a 10 dL. Veja a justificativa:
1 dL -------------- 0,1 L
x dL -------------- 1 L
x = 1/0,1 = 10 dL
Portanto, podemos dizer que:
365 mL = 0,365 L
0,365 L = 0,365 x 1 L
0,365 x 1 L = 0,365 x 10 dL
Ou seja,
365 mL = 3,65 dL.
Para fazer a conversão por meio de operações sucessivas, precisamos entender que a unidade dL está duas casas acima da unidade mL, portanto, são necessárias duas divisões sucessivas por 10 (ou seja, por 100) para converter mililitros em decilitros.
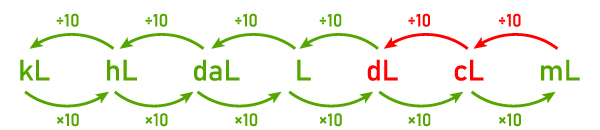
Assim, 365 mL é igual a 365/100 dL, que é igual a 3,65 dL.
-
Conversão entre unidades do litro e unidades cúbicas
As unidades cúbicas são medidas tridimensionais, obtidas a partir do cálculo das dimensões de figuras geométricas, no caso, comprimento, largura e altura.
Por exemplo, dado um cubo de lado igual a 1 metro (1 m), o seu volume é calculado:
Volume do cubo = lado x lado x lado = (lado)3 = (1 m)3 = 1 m x 1 m x 1 m = 1 m3
Assim como ocorre com a unidade de área, devemos nos atentar ao fato de que a unidade é elevada ao cubo, portanto, a conversão ocorre por meio da multiplicação ou divisão por 1000 (10³), pois:
1 m3 = 1 m x 1 m x 1 m = 100 cm x 100 cm x 100 cm = (100 cm)3 = 106 cm3
A conversão entre as unidades do litro (e seus respectivos múltiplos e submúltiplos) e as unidades cúbicas partem do seguinte pressuposto:
- 1 cm3 = 1 mL
- 1 dm³ = (10 cm)3 = 1000 cm3 = 1000 mL = 1 L
- 1 m³ = (10 dm)3 = 1000 dm3 = 1000 L
Vejamos um caso de conversão para fixação das unidades cúbicas.
Exemplo 1:
- Converter 5000 m3 em litros:
Cada 1 m3 equivale a 1000 dm3, portanto, 5000 m3 são:
5000 x 1000 dm3
Porém, 1 dm3 equivale a 1 L e, portanto, 1000 dm3 são 1000 L.
Por isso,
5000 m3 = 5000 x 1000 dm3 = 5000 x 1000 L = 5000000 L
Conversão de medidas de tempo
Dentro das unidades de tempo, temos como unidade fundamental o segundo, cujo símbolo é “s”. Diferentemente dos casos anteriores, os múltiplos do segundo não se alcançam por operações com bases de 10, apenas seus submúltiplos.
Dentre os submúltiplos do segundo, temos:
- 1 milissegundo (ms) = 0,001 s, ou seja, um milésimo de segundo.
- 1 microssegundo (µs) = 0,000001 s, ou seja, um milionésimo de segundo.
- 1 nanossegundo (ns) = 0,000000001 s, ou seja, um bilionésimo de segundo.
Os múltiplos do segundo, entretanto, trabalham no chamado sistema sexagesimal babilônico, ou seja, na base de 60.
- 1 minuto (m ou min) = 60 s
- 1 hora (h) = 60 min = 3600 s
Já o sistema de tempo baseado no calendário (gregoriano), tem como base, por sua vez, o movimento da Terra ao redor do Sol, dessa forma, temos:
- 1 dia = 24 horas
- 1 semana = 7 dias
- 1 mês = 30 dias (em média)
- 1 ano = 365 dias (valor aproximado).
A multiplicidade com bases de 10 retorna quando trazemos as unidades de tempo baseadas em anos (década, século e milênio):
- 1 década = 10 anos
- 1 século = 100 anos
- 1 milênio = 1000 anos
Vejamos alguns exemplos práticos.
- Qual a duração de 1 ano em segundos?
1 ano possui 365 dias, e cada dia tem 24 horas. Cada hora possui 60 minutos e cada minuto tem 60 segundos. Portanto, a duração de 1 ano em segundos é igual a:
1 x 365 x 24 x 60 x 60 = 31536000
Ou seja, um ano equivale a 31.536.000 segundos.
- Qual a duração de 3 semanas em horas?
Cada semana possui 7 dias, e cada dia tem 24 horas. Portanto, três semanas têm:
3 x 7 x 24 horas = 504 horas
Ou seja, três semanas equivalem a 504 horas.
Conversão de medidas de área
As unidades de área são derivadas das unidades de comprimento, uma vez que a área é a medida da superfície de uma figura bidimensional, composta por comprimento e largura. Tendo como referência um quadrado hipotético de lado igual a 1 metro, pode-se dizer que a área deste quadrado é igual a:
Área do quadrado = lado x lado = (lado)² = 1 m x 1m = 1 m2.
Ou seja, a área é o produto de duas dimensões de comprimento e, por conta disso, sua unidade fundamental é o metro quadrado, representado por m2.
A questão envolvendo unidades de área é justamente o fato de o valor do metro estar elevado ao quadrado. Dessa forma, não podemos dizer que 1 m2 é igual a 100 cm2, mas sim igual a 10000 cm2, pois:
1 m2 = 1 m x 1 m = 100 cm x 100 cm = 10000 cm2
Assim, a conversão de múltiplos e submúltiplos de área, em termos de m2, ocorre em bases de 100 (ou seja, 102).
Por isso, podemos dizer que:
|
Unidade fundamental |
Unidade |
Símbolo |
Conversão |
|
1 metro quadrado (m2) |
quilômetro quadrado |
km2 |
1 km2 = 106 m2 |
|
hectômetro quadrado |
hm2 |
1 hm2 = 104 m2 |
|
|
decâmetro quadrado |
dam2 |
1 dam2 = 102 m2 |
|
|
decímetro quadrado |
dm2 |
1 dm2 = 10−2 m2 |
|
|
centímetro quadrado |
cm2 |
1 cm2 = 10−4 m2 |
|
|
milímetro quadrado |
mm2 |
1 mm2 = 10−6 m2 |
Vejamos alguns exemplos práticos:
- Como converter 5 quilômetros quadrados de área em decímetro quadrado:
Cada 1 km2 equivale a 106 m2. Isso quer dizer que 5 km2 são 5 x 106 m2.
Da mesma forma, cada 1 dm2 equivale a 10−2 m2. Com isso, entendemos que 1 m2 equivale a 100 dm2.
Portanto, podemos raciocinar da seguinte forma:
5 km2 = 5 x 106 m2 = 5 x 106 x 100 dm2 = 5 x 106 x 102 dm2 = 5 x 108 dm2.
- Como converter 2,5 centímetros quadrados em decâmetros quadrados:
Cada 1 cm2 equivale a 10−4 m2, o que quer dizer que 1 m2 equivale a 104 cm2.
Cada 1 dam2 equivale a 102 m2, ou seja, 1 m2 equivale a 10−2 dam2.
Portanto:
2,5 cm2 = 2,5 x 10−4 m2 = 2,5 x 10−4 x 10−2 dam2 = 2,5 x 10−6 dam2.
→ Conversão de outras medidas de área
Dentro, ainda, do sistema métrico, é possível citar o hectare (ha), medida muito utilizada no campo agrícola:
- 1 hectare (ha) = 10000 m2
Para o sistema imperial de medidas, valem também as seguintes conversões:
- 1 pé quadrado = 0,092903 m2
- 1 polegada quadrado = 0,00064516 m2
- 1 milha quadrado = 2,59 x 106 m2
- 1 jarda quadrado = 0,836127 m2
Outra unidade de medida de área conhecida é o “acre”, muito usado no sistema britânico e no sistema norte-americano:
- 1 acre = 4046,86 m2
Conversão de medidas de temperatura
Existem duas unidades básicas de temperatura: Celsius, representada por °C, e Fahrenheit, representada por °F. A escala Celsius divide o intervalo líquido da água, na pressão do nível do mar, em 100 unidades. Assim, a temperatura de 0 °C corresponde ao ponto de fusão da água na pressão do nível do mar (1 atmosfera de pressão) e a temperatura de 100 °C corresponde ao ponto de ebulição da água na pressão do nível do mar.
Já a escala Fahrenheit divide o intervalo líquido da água, na pressão do nível do mar, em 180 unidades. O ponto de fusão da água corresponde aos 32 °F, enquanto o ponto de ebulição da água corresponde aos 212 °F.
Assim, cada 1 °C corresponde a 1,8 °F. A conversão entre Celsius e Fahrenheit é dada pela seguinte expressão:
T (°C) = [T (°F) – 32]/1,8
ou
T (°F) = [T (°C) x 1,8] + 32
Vejamos exemplos de aplicação dessas fórmulas:
Exemplo 1:
- Convertendo 46 °C em °F:
Aplicando a fórmula, escrevemos:
T (°F) = (46 x 1,8) + 32
T (°F) = 82,8 + 32
T (°F) = 114,8 °F
Exemplo 2:
- Convertendo 10 °F em °C:
Aplicando a fórmula, escrevemos:
T (°C) = (10 – 32)/1,8
T (°C) = –22/1,8
T (°C) \(\cong\) –12,2 °C
Existem também as escalas absolutas de temperatura, as quais não aceitam valores negativos de temperatura. Elas se iniciam a partir do zero absoluto, o menor valor possível de temperatura, segundo as leis da termodinâmica, no qual não existe qualquer movimento molecular.
Associada à escala Celsius, temos a escala Kelvin (K) cuja conversão ocorre mediante a seguinte expressão:
T (K) = T (°C) + 273,15
Associada à escala Fahrenheit, temos a escala Rankine (R ou Ra) cuja conversão ocorre mediante a seguinte expressão:
T (R) = T (°F) + 459,67
Conversão de medidas de velocidade
Segundo a Física, entende-se como velocidade o espaço deslocado por um corpo em um determinado intervalo de tempo. Dessa forma, a unidade de velocidade é composta por uma unidade de comprimento dividida por uma unidade de tempo. Por isso, para fazer a correta conversão entre unidades de medidas de velocidade, deve-se converter, ao mesmo tempo, a unidade de comprimento e a unidade de tempo.
Exemplo:
Vejamos o caso em que um valor de velocidade é dado em quilômetros por hora (km/h). Para se converter tal valor em metro por segundo (m/s), devemos converter, ao mesmo tempo, o quilômetro em metro e a hora em segundo.
Assim:
\(1 \frac{km}{h} = 1 \times \frac{1000m}{3600s} = \frac{1}{3,6} \frac{m}{s}\)
Ou seja, para se converter um valor de km/h para m/s, devemos pegar o valor da velocidade e dividir por 3,6.
Exemplo: Um carro viaja a uma velocidade de 80 km/h, quanto isso seria em m/s?
Faremos a divisão de 80/3,6, o que corresponde a, aproximadamente, 22,2 m/s.
Sistema internacional de unidades
O Sistema Internacional de Unidades (SI) é um sistema que foi desenvolvido e estabelecido em 1960, na reunião da 11ª Conferência Geral de Pesos e Medidas (CGPM). A ideia era criar um sistema de unidades coerente para a utilização em todos os aspectos da vida, como comércio internacional, produção industrial, saúde e segurança, proteção do meio ambiente, além da ciência fundamental.
As definições das unidades do SI são estabelecidas a partir de um conjunto de sete constantes definidoras da Física, das quais se deduzem todas as unidades de base do sistema, apresentadas na tabela a seguir:
|
Grandeza de base |
Unidade |
Símbolo |
|
tempo |
segundo |
s |
|
comprimento |
metro |
m |
|
massa |
quilograma |
kg |
|
corrente elétrica |
ampere |
A |
|
temperatura |
kelvin |
K |
|
quantidade de matéria |
mol |
mol |
|
intensidade luminosa |
candela |
cd |
A partir das unidades de base, é possível, portanto, definir as unidades derivadas, que são produtos de potências das unidades de base.
Por exemplo, a unidade de base para comprimento, segundo o SI, é o metro (m). Assim, a unidade derivada para área, segundo o SI, é o metro quadrado (m2). Se a unidade SI para comprimento é metro (m) e a unidade SI para tempo é segundo (s), logo, a unidade SI para velocidade é o metro por segundo (m/s).
A força, segundo as Leis de Newton, é calculada como sendo o produto da massa pela aceleração. A aceleração é a taxa da variação de velocidade de um corpo dentro de um intervalo de tempo. Assim, a aceleração é entendida como uma unidade de velocidade, dividida por uma unidade de tempo, que no SI seria (m/s)/s, que é igual a m/s2. Se força é o produto da massa pela aceleração, então a unidade SI para a força é kg ∙ m/s2, que é conhecida como newton e é representada por N.
Já o trabalho mecânico, corresponde à aplicação de 1 N de força a um objeto na distância de 1 metro. Assim, no SI, a unidade de trabalho mecânico é o N ∙ m, ou kg ∙ m2/s2. Essa unidade é conhecida como joule, sendo representada pela letra J, também aplicada como unidade SI para energia e calor.
Saiba mais: Análise dimensional — ferramenta que determina a unidade de medida de uma grandeza
Exercícios resolvidos sobre conversão de medidas
Questão 1. (ENEM/2020) Pesquisadores da Universidade de Tecnologia de Viena, na Áustria, produziram miniaturas de objetos em impressoras 3D de alta precisão. Ao serem ativadas, tais impressoras lançam feixes de laser sobre um tipo de resina, esculpindo o objeto desejado. O produto final da impressão é uma escultura microscópica de três dimensões, como visto na imagem ampliada.

A escultura apresentada é uma miniatura de um carro de Fórmula 1, com 100 micrômetros de comprimento. Um micrômetro é a milionésima parte de um metro.
Usando notação científica, qual é a representação do comprimento dessa miniatura, em metro?
A) 1,0 x 10−1
B) 1,0 x 10−3
C) 1,0 x 10−4
D) 1,0 x 10−6
E) 1,0 x 10−7
Resposta: Letra C
100 micrômetros correspondem a 100 × 10−6 metros, pois o micrômetro é a milionésima parte de um metro (1 dividido por 1000000). Como 100 corresponde a 102, o valor, em metro e usando notação científica é igual a 1,0 x 102 x 10−6, ou seja, 1,0 x 10−4 metros.
Questão 2. (ENEM PPL/2019) O projeto de transposição do Rio São Francisco consiste na tentativa de solucionar um problema que há muito afeta as populações do semiárido brasileiro, a seca. O projeto prevê a retirada de 26,4 m3/s de água desse rio. Para tornar mais compreensível a informação do volume de água a ser retirado, deseja-se expressar essa quantidade em litro por minuto.
Disponível em: www.infoescola.com. Acesso em: 28 out. 2015.
Com base nas informações, qual expressão representa a quantidade de água retirada, em litro por minuto?
A) (26,4/1000) x 60
B) (26,4/10) x 60
C) 26,4 x 1 x 60
D) 26,4 x 10 x 60
E) 26,4 x 1000 x 60
Resposta: Letra E
1 m3 corresponde a 1000 litros. Da mesma forma, em 1 minuto estão 60 segundos, o que quer dizer que 1 segundo corresponde a 1/60 minuto.
Assim:
\(26,4 \, \frac{m^3}{s} = \frac{26,4 \times 1000L}{\frac{1}{60}min} = 26,4 \times 1000 \times 60 \, \text{L}/\text{min} \)
Fontes
INSTITUTO NACIONAL DE METROLOGIA, QUALIDADE E TECNOLOGIA (INMETRO); INSTITUTO PORTUGUÊS DE QUALIDADE (IPQ). Sistema Internacional de Unidades (SI). 2ª edição da tradução luso-brasileira. Brasília, DF: Inmetro, 2025.
INTERNATIONAL SOCIETY OF AUTOMATION. Units Conversion Tables. ISA. Disponível em: https://www.isa.org/getmedia/5be3daca-5c44-4d9e-bf1c-a4aa55cfb759/CCST-Conversions-document.pdf
NATIONAL INSTITUTE OF STANDARDS AND TECHNOLOGY. Unit conversion. NIST. Disponível em: https://www.nist.gov/pml/owm/metric-si/unit-conversion
.jpg)

