Transformações Gasosas: Exercícios Resolvidos.

Sabemos que as transformações gasosas podem ser:

Isocórica

Transformação em que o volume do gás permanece constante.



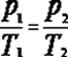
Isotérmica

Transformação em que a temperatura permanece constante.



Isobárica

Transformação em que a pressão permanece constante.



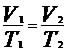
Vejamos agora algumas aplicações dessas equações em exercícios:

1) (FUVEST – SP) Um recipiente indeformável, hermeticamente fechado, contém 10 litros de um gás perfeito a 30 ºC, suportando a pressão de 2 atmosferas. A temperatura do gás é aumentada até atingir 60º C.
a) Calcule a pressão final do gás.
b) Esboce o gráfico pressão versus temperatura da transformação descrita.

Solução:

Letra a)
Considerando-se que o volume do gás é constante, temos que a transformação é isocórica.
Assim,


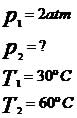
Substituindo os valores fornecidos pelo problema na equação da transformação isocórica, temos:



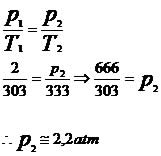
Assim, podemos concluir que a pressão e a temperatura são grandezas diretamente proporcionais.

Letra b)
A partir da resolução do item anterior, podemos esboçar o gráfico da pressão em função da temperatura (pressão x temperatura).
 

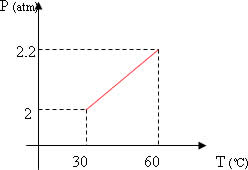
2) (FAAP – SP) A 27º C, um gás ideal ocupa 500 cm3. Que volume ocupará a -73º C, sendo a transformação isobárica?

Sabe-se que:

T₁ = 27º C = 300 K
T₂ = -73 ºC = 200 K
V₁ = 500 cm³
V₂ = ?
Da transformação isobárica temos que:

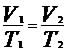, assim:
 

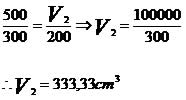
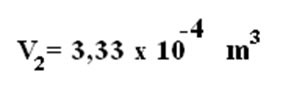
Podemos concluir que, para a transformação isobárica, o volume e a temperatura são diretamente proporcionais.

3) (UNIMEP – SP) 15 litros de uma determinada massa gasosa encontram-se a uma pressão de 8,0 atm e à temperatura de 30º C. Ao sofrer uma expansão isotérmica, seu volume passa a 20 litros. Qual será a nova pressão do gás?

Do enunciado temos:

V₁ = 15 litros
V₂ = 20 litros
P₁ = 8,0 atm
P₂ = ?
T = 30º C = 303 K (TEMPERATURA CONSTANTE)

Utilizando a equação da transformação isotérmica, temos:



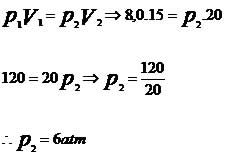
De acordo com a transformação isotérmica, a pressão e o volume, em uma transformação gasosa, são grandezas inversamente proporcionais.

*Obs.: Para a solução de problemas envolvendo as transformações gasosas devemos utilizar SEMPRE a temperatura na escala absoluta (Kelvin).
 

Por Kleber Cavalcante
Graduado em Física
Equipe Brasil Escola

Veja mais!!!

As Transformações Gasosas
Veja como ocorre cada uma das transformações.

Termologia - Física - Brasil Escola