Seno, cosseno e tangente

Seno, cosseno e tangente são os nomes dados às razões trigonométricas. Grande parte dos problemas que envolvem cálculos de distância é resolvida utilizando-se a trigonometria. E para isso, é muito importante compreender seus fundamentos, começando pelo triângulo retângulo.

As razões trigonométricas são também muito importantes, pois elas relacionam as medidas de dois lados do triângulo com um dos ângulos agudos, associando essa relação com um número real.

Veja mais: Identificando os quadrantes do ciclo trigonométrico

Tópicos deste artigo

• 1 - Características do triângulo retângulo
• 2 - Seno
• 3 - Cosseno
• 4 - Tangente
• 5 - Relação entre seno, cosseno e tangente
• 6 - Tabelas trigonométricas
• 7 - Exercícios resolvidos sobre seno, cosseno e tangente

Características do triângulo retângulo

O triângulo retângulo é formado por um ângulo de 90° (ângulo reto). Os demais ângulos são menores que 90º, ou seja, são agudos, e, além disso, sabemos que os maiores lados estão sempre opostos aos maiores ângulos. No triângulo retângulo, o maior lado é chamado de hipotenusa e está “à frente” do ângulo reto, os demais lados são chamados de catetos.

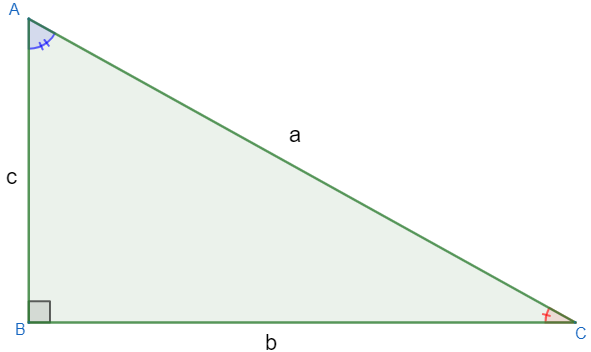
No triângulo acima, temos que os lados que medem c e b são os catetos, e o lado que mede a é a hipotenusa. Em todo triângulo retângulo, a relação conhecia como teorema de Pitágoras é válida.

a² = b² + c²           

Os catetos, daqui em diante, também receberão nomes especiais. As nomenclaturas dos catetos dependerão do ângulo de referência. Considerando o ângulo em azul na imagem acima, temos que o cateto que mede b é o cateto oposto, e o cateto que está ao lado do ângulo, ou seja, que mede c é o cateto adjacente.

Seno

Antes de definir uma fórmula para o seno de um ângulo, vamos entender a ideia de seno. Imagine uma rampa, nela podemos determinar a razão entre a altura e o percurso, certo? Essa razão chamaremos de seno do ângulo α.

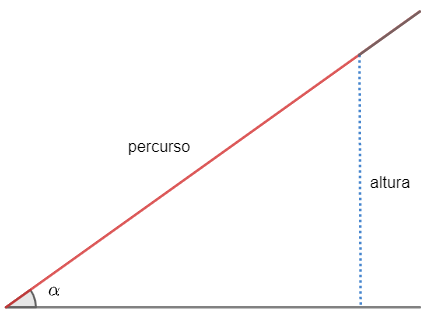
Assim,

sen α =   altura 
             percurso 

Cosseno

De maneira análoga à ideia do seno, temos o sentido do cosseno, entretanto, em uma rampa, o cosseno é a razão entre o afastamento em relação ao solo e o percurso na rampa.

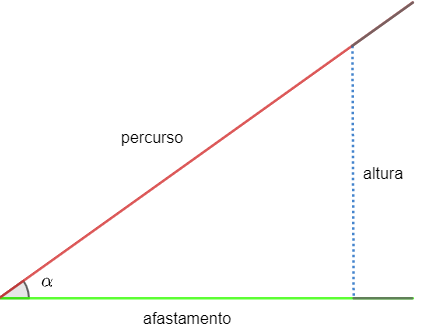
Assim:

cos α = afastamento
              percurso

Tangente

Também de modo semelhante às ideias de seno e cosseno, a tangente é a razão entre a altura e o afastamento de uma rampa. 

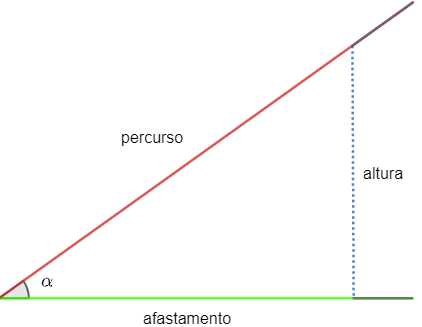
Assim:

tg α = altura
        afastamento

A tangente fornece-nos o índice de subida.

Leia também: Trigonometria em um triângulo qualquer

Relação entre seno, cosseno e tangente

De modo geral, podemos definir então seno, cosseno e tangente em um triangulo retângulo qualquer utilizando as ideias anteriores. Veja a seguir:

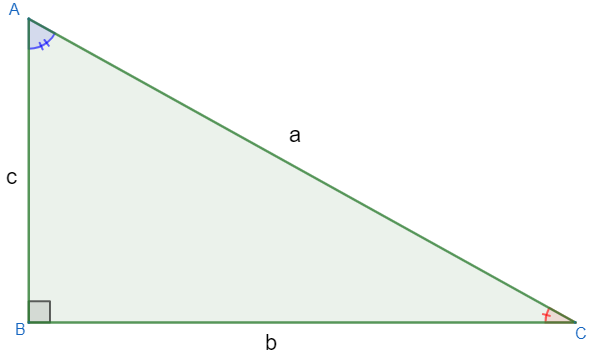
Tomando primeiramente o ângulo α como referencial, temos:

sen α =   Cateto oposto  =  c
                 Hipotenusa         a

cos α =   Cateto adjacente  =  b
                     Hipotenusa          a

tg α =   Cateto oposto       =     c
           Cateto adjacente           b

Tomando agora o ângulo β como referencial, temos:

sen β =   Cateto oposto  =  b
                Hipotenusa          a

cos β =   Cateto adjacente  =  c
                     Hipotenusa          a

tg β =   Cateto oposto       = b
            Cateto adjacente      c

Tabelas trigonométricas

Existem três valores de ângulos que devemos saber. São eles:

Os demais valores são dados nos enunciados dos exercícios ou podem ser conferidos na tabela seguinte, mas não se preocupe, não é necessário tê-los memorizados (exceto os da tabela anterior).

Saiba também: Secante, cossecante e cotangente

Exercícios resolvidos sobre seno, cosseno e tangente

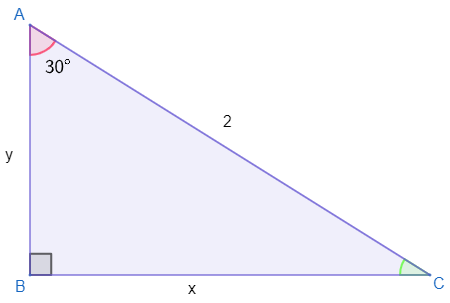
Questão 1 -  Determine o valor de x e y no triângulo a seguir.

Solução:

Veja no triângulo que o ângulo dado foi de 30°. Observando ainda o triângulo, temos que o lado que mede x é o cateto oposto ao ângulo de 30°, e o lado que mede y é o cateto adjacente ao ângulo de 30°. Assim, devemos buscar uma razão trigonométrica que relacione o que procuramos com que é dado (hipotenusa). Logo:

sen 30° =   Cateto oposto 
                    Hipotenusa    

cos 30° =   Cateto adjacente 
                      Hipotenusa      

Determinado o valor de x:

sen 30° =  Cateto oposto 
                            Hipotenusa           

sen 30° =  x
                  2

Olhando na tabela, temos que:

sen 30° = 1
                 2

Substituindo na equação, teremos:

1 = x
2    2

x = 1

De modo análogo, consideraremos

Assim: 

Cos 30° = √3 
                  2

cos 30° =   Cateto adjacente 
                       Hipotenusa 

cos 30° = Y
                     2     

√3 = Y
 2     2

y = √3

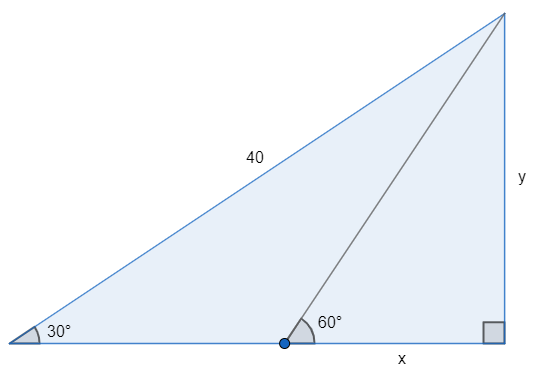
Questão 2 – (PUC-SP) Qual é o valor de x na figura seguinte?

Solução:

Visualizando o triângulo maior, observe que y é oposto ao ângulo de 30° e que 40 é a hipotenusa, ou seja, podemos usar a razão trigonométrica seno.

sen 30° = Y
               40

    1   =  Y
     2      40

    2 y = 40
     y = 20

Olhando agora para o triângulo menor, veja que temos o valor do cateto oposto e buscamos o valor de x, que é o cateto adjacente. A relação trigonométrica que envolve esses dois catetos é a tangente. Assim:

tg 60°  = 20
               x

√3= 20
       x

√3 x = 20

x = 20  ·  √3
     √3     √3

x = 20√3
       3