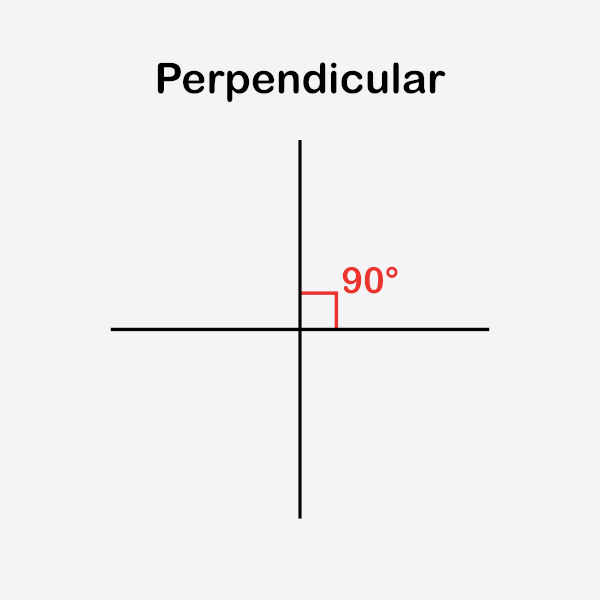
Retas perpendiculares

Retas perpendiculares são aquelas que formam entre si um ângulo de 90º. Podemos representar duas retas perpendiculares no Plano Cartesiano.

Quando representamos a equação de duas retas, para saber se elas são perpendiculares, é necessário verificar se o coeficiente angular de uma delas é igual ao oposto do inverso da outra. Dessa forma, se \(m_1\) é o coeficiente angular de uma das retas, o coeficiente angular da outra será \(-\frac{1}{m_1}\); em duas retas perpendiculares, o produto dos seus coeficientes angulares é igual a \( -1\).

Leia também: Posições relativas entre reta e plano

Tópicos deste artigo

• 1 - Resumo sobre retas perpendiculares
• 2 - O que são retas perpendiculares?
• 3 - Retas perpendiculares no Plano Cartesiano
• 4 - Coeficiente angular de retas perpendiculares
• 5 - Como saber se duas retas são perpendiculares entre si?
  • Método prático
• 6 - Exercícios resolvidos sobre retas perpendiculares

Resumo sobre retas perpendiculares

• As retas perpendiculares formam um ângulo de 90º quando se cruzam.

• Podemos representar duas retas perpendiculares no Plano Cartesiano.

• Conhecendo a equação das retas \( r_1\) e \(r_2\), elas são perpendiculares se:

  • o produto dos seus coeficientes for igual \( -1\):

\(m_1\cdot m_2=-1\)

• • o coeficiente angular de uma for igual ao oposto do inverso do coeficiente angular da outra:

\(m_1=-\frac{1}{m_1}\)

O que são retas perpendiculares?

Quando comparamos duas retas pertencentes ao mesmo plano, existe o que conhecemos como posições relativas entre duas retas. As retas perpendiculares são um desses casos.

Quando as retas se cruzam, elas são conhecidas como concorrentes, e quando elas se cruzam formando um ângulo reto, ou seja, um ângulo de 90°, essas retas concorrentes são conhecidas também como perpendiculares, então podemos afirmar que:

Veja, a seguir, a representação de duas retas perpendiculares:

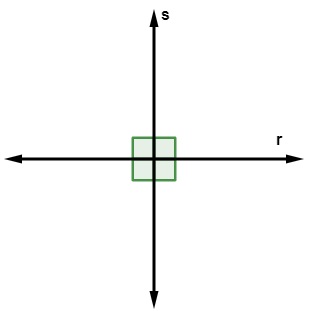
Retas perpendiculares no Plano Cartesiano

Quando as retas são representadas no Plano Cartesiano, podemos realizar o estudo das retas perpendiculares de forma analítica. A geometria analítica busca descrever de forma algébrica os objetos da geometria.

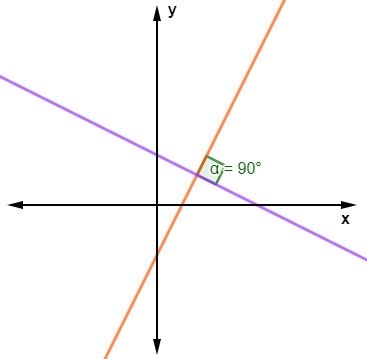
Quando analisamos algebricamente a equação de duas retas perpendiculares, é possível desenvolver um método para verificar se elas são perpendiculares ou não.

Coeficiente angular de retas perpendiculares

Ao analisar-se o coeficiente angular de duas retas perpendiculares, percebe-se uma relação importante que acaba se tornando um método para verificar se duas retas são perpendiculares ou não.

Conhecendo a equação da reta, duas retas são perpendiculares se o coeficiente angular de uma delas for igual ao oposto do inverso do coeficiente angular da outra. Conhecemos como oposto de um número o número com o sinal trocado, e como seu inverso, a fração que tem o numerador igual a 1 e o denominador igual a esse número.

Então, dadas a reta \(r_1\) com coeficiente angular \(m_1\) e a reta \(r_2\) com coeficiente angular \(m_2\), essas retas são perpendiculares se:

\(m_2=-\frac{1}{m_1}\)

Como saber se duas retas são perpendiculares entre si?

Dadas duas retas \(r_1\) e \(r_2\), com coeficiente angular \(m_1\) e \(m_2\)  respectivamente, para saber se elas são perpendiculares, basta verificar se:

\(m_2=-\frac{1}{m_1}\)

Podemos verificar também, utilizando o produto entre os coeficientes angulares, se as retas são perpendiculares se:

\(m_1\cdot m_2=-1\)

Exemplo:

As retas de equação \(r_1\): 2x + 3y + 4 = 0 e \(r_2\): -3x + 2y – 1 = 0 são perpendiculares?

Resolução:

Transformaremos a equação geral da reta na equação reduzida da reta para encontrarmos o coeficiente angular da reta:

\(3y=-2x-4\ \)

\(y=-\frac{2}{3}x-\frac{4}{3}\)

Então encontramos o coeficiente angular da reta \(r_1\):

\(m_1=-\frac{2}{3}\)

Agora encontraremos \(m_2\):

\(2y=3x+1\ \)

\(y=\frac{3}{2}x+\frac{1}{2}\)

Então o coeficiente angular da reta \(r_2\) é:

\(m_2=\frac{3}{2}\)

Para verificar se as retas são perpendiculares, multiplicaremos os coeficientes angulares:

\(m_1\cdot m_2=-\frac{2}{3}\cdot\frac{3}{2}=-1\)

Como o produto é igual a -1, então essas retas são perpendiculares.

• Método prático

Para que não seja necessário encontrar a equação reduzida da reta, quando conhecemos a equação geral da reta, é possível verificar se as retas são perpendiculares ou não com base nos coeficientes a e b de cada uma das equações.

Conhecemos as duas equações:

\(r_1=a_1x+b_1y+c_1\)

\(r_2=a_2x+b_2y+c_2\)

Duas retas são perpendiculares se e somente se:

\(a_1\cdot a_2+b_1\cdot b_2=0\)

Exemplo:

Verifique se as retas \(r_1\) = x + 2y – 3 = 0 e \(r_2\) = -2x + y = são perpendiculares por meio do método prático.

Resolução:

Temos que: \(a_1=1\), \(b_1=2\), \(a_2=-2\) e \(b_2=1\)

Então, pelo método prático:

\(a_1\cdot a_2+b_1\cdot b_2=0\)

\(1\cdot\left(-2\right)+2\cdot1=0\)

\(-2+2=0\ \)

\(0=0\)

Desse modo, as retas são perpendiculares.

Leia também: Ponto de interseção entre duas retas

Exercícios resolvidos sobre retas perpendiculares

Questão 1

Duas retas concorrentes são consideradas perpendiculares quando:

A) não possuem nenhum ponto em comum.

B) possuem mais de um ponto em comum.

C) formam um ângulo reto entre elas.

D) possuem infinitos pontos em comum.

E) formam um ângulo de 180º entre elas.

Resolução:

Alternativa C

Duas retas são perpendiculares se elas formam um ângulo de 90°, ou seja, um ângulo reto.

Questão 2

A reta \( r_2\) é perpendicular à reta \( r_1\): \(x+2y-3=0\),  então o coeficiente angular da reta \(r_2\) é:

A) -1

B) 1

C) 2

D) -2

E) \(\frac{1}{2}\)

Resolução:

Alternativa C

Primeiro encontraremos o coeficiente angular da reta \(r_1\).

Isolando o y:

2y = -x + 3

\(y=\frac{-x}{2}+\frac{3}{2}\)

Então \(m_1=-\frac{1}{2}\)

Sabemos que:

\(m_1\cdot m_2=-1\)

\(-\frac{1}{2}m_2=-1\)

\(m_2=-1\cdot\left(-2\right)\)

\(m_2=2\)

Por Raul Rodrigues de Oliveira
Professor de Matemática