Centro de gravidade

O centro de gravidade é o ponto em um corpo onde considera-se que está a força da gravidade de todo o corpo. Assim, ao considerar as forças gravitacionais entre um planeta e uma estrela, por exemplo, os únicos pontos a serem considerados na interação são os centros de gravidade do planeta e da estrela, pouco importando o formato e a distribuição de massas deles.

Leia também: Afinal, o que é gravidade?

Tópicos deste artigo

• 1 - Resumo sobre centro de gravidade
• 2 - O que é o centro de gravidade?
• 3 - Onde fica o centro de gravidade?
  • → Centro de gravidade do corpo humano
  • → Centro de gravidade do planeta Terra
• 4 - Fórmula do centro de gravidade
• 5 - Diferenças entre centro de gravidade e centro de massa
• 6 - Equilíbrio e centro de gravidade
• 7 - Exercícios resolvidos sobre centro de gravidade

Resumo sobre centro de gravidade

• O centro de gravidade de um corpo é o ponto onde a força gravitacional age efetivamente no corpo.
• Centro de gravidade do corpo humano: em posição neutra, está na região inguinal; com braços erguidos, sobe para o umbigo; ao curvar o corpo, desloca-se para baixo.
• Centro de gravidade do planeta Terra: no centro do núcleo interno.
• O centro de gravidade é onde a força gravitacional atua, enquanto o centro de massa é o ponto onde a massa do corpo pode ser considerada concentrada. Em corpos pequenos, os dois coincidem.
• Fórmula do centro de gravidade no eixo x: \(x_{CG} = \frac{m_1 \cdot x_1 + m_2 \cdot x_2 + m_3 \cdot x_3 + \dots + m_n \cdot x_n}{m_1 + m_2 + m_3 + \dots + m_n} \).
• É possível encontrar o centro de gravidade de um corpo deixando-o em equilíbrio e traçando retas verticais. O cruzamento das retas indica a posição do centro de gravidade.

O que é o centro de gravidade?

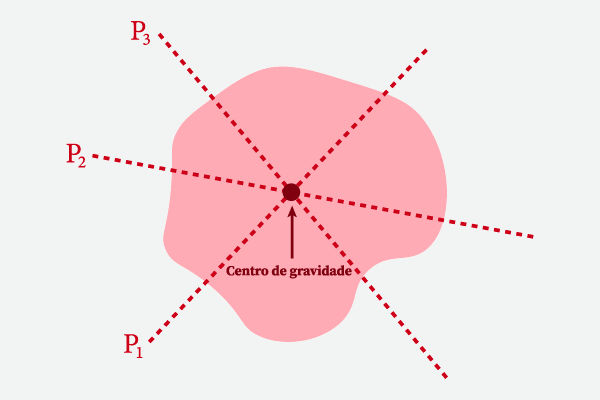
O centro de gravidade é o ponto em um corpo onde pode se encontra a força da gravidade de todo o corpo. A força gravitacional que age sobre um corpo é a soma vetorial das forças gravitacionais que agem sobre cada átomo desse corpo. Assim, em vez de considerar cada átomo, podemos considerar que a força gravitacional age efetivamente sobre um único ponto de um corpo, esse ponto é denominado o centro de gravidade (CG) do corpo, ou baricentro.

Onde fica o centro de gravidade?

→ Centro de gravidade do corpo humano

O centro de gravidade do corpo humano vai depender de cada indivíduo, de como a sua massa está distribuída, sua altura, curvaturas e posturas. Normalmente o centro de gravidade das mulheres está mais abaixo do que dos homens, devido a um maior acúmulo de massa, em média, no quadril e nas pernas, enquanto, nos homens, há maior acúmulo de massa na região do peitoral, costas e braços.

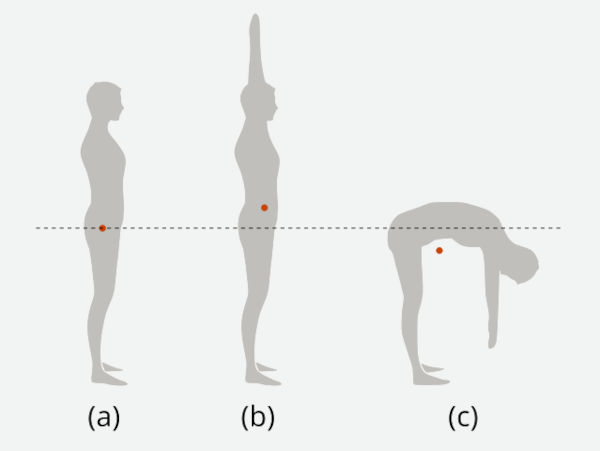
Considerando um ser humano adulto médio de 70 kg, podemos ver na figura (a) que, em uma posição neutra, o centro de gravidade está localizado na região inguinal. Na figura (b), notamos que, com os braços levantados, o centro de gravidade sobe levemente para a região do umbigo. Na figura (c), com o corpo curvado e os braços direcionados para baixo, o centro de gravidade é deslocado para baixo e posicionado em uma região que não há parte do corpo.

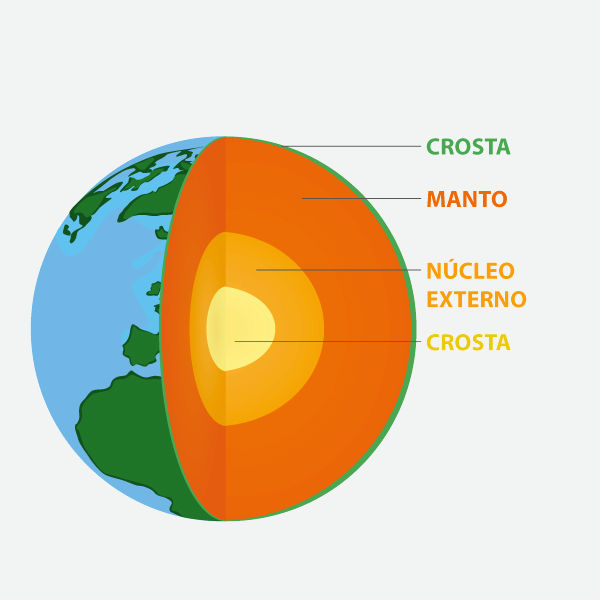
→ Centro de gravidade do planeta Terra

Devido a sua distribuição simétrica de massa e formato esférico também simétrico, é possível provar que o centro de gravidade do planeta Terra está localizado no centro da Terra, mais especificamente no centro do núcleo interno terrestre. Assim, os fenômenos gravitacionais envolvendo o planeta Terra, como a interação Sol-Terra ou Terra-Lua, podem ser considerados nesse ponto central.

Fórmula do centro de gravidade

Para n partículas, a posição do centro de gravidade (CG) no eixo x é dada por:

\(x_{CG} = \frac{m_1 \cdot x_1 + m_2 \cdot x_2 + m_3 \cdot x_3 + \dots + m_n \cdot x_n}{m_1 + m_2 + m_3 + \dots + m_n} \)

• m → massa da partícula
• x → sua posição no eixo x

Da mesma forma, a posição do centro de gravidade no eixo y é:

\(y_{CG} = \frac{m_1 \cdot y_1 + m_2 \cdot y_2 + m_3 \cdot y_3 + \dots + m_n \cdot y_n}{m_1 + m_2 + m_3 + \dots + m_n} \)

• m → massa da partícula
• y  → sua posição no eixo y

Por fim, a posição do centro de gravidade no eixo z é também escrita como:

\(z_{CG} = \frac{m_1 \cdot z_1 + m_2 \cdot z_2 + m_3 \cdot z_3 + \dots + m_n \cdot z_n}{m_1 + m_2 + m_3 + \dots + m_n} \)

• m → massa da partícula
• z → sua posição no eixo z

Diferenças entre centro de gravidade e centro de massa

Enquanto o centro de gravidade é o ponto onde pode ser considerada a força da gravidade de todo o corpo, o centro de massa é o ponto que se move como se toda a massa do sistema estivesse concentrada nesse ponto. Se as dimensões do corpo forem pequenas em comparação ao tamanho do planeta Terra, a gravidade será igual para todos os átomos do corpo, então o centro de gravidade do corpo coincidirá com o centro de massa.

Acesse também: Centro de massa — mais detalhes sobre esse ponto

Equilíbrio e centro de gravidade

É possível encontrar o centro de gravidade de um corpo, sem fazer cálculos, usando apenas o equilíbrio. O experimento funciona da seguinte forma: inicialmente suspendemos o corpo por um ponto qualquer e o deixamos atingir a posição de equilíbrio, marcando uma reta vertical para baixo, na direção da força gravitacional.

Em seguida, suspendemos o corpo por outro ponto e novamente o deixamos atingir a posição de equilíbrio, marcando uma outra reta vertical para baixo. Façamos isso quantas vezes for necessário, até que o cruzamento das retas indicará um ponto. O centro de gravidade do corpo estará justamente nesse ponto que surge no cruzamento das retas.

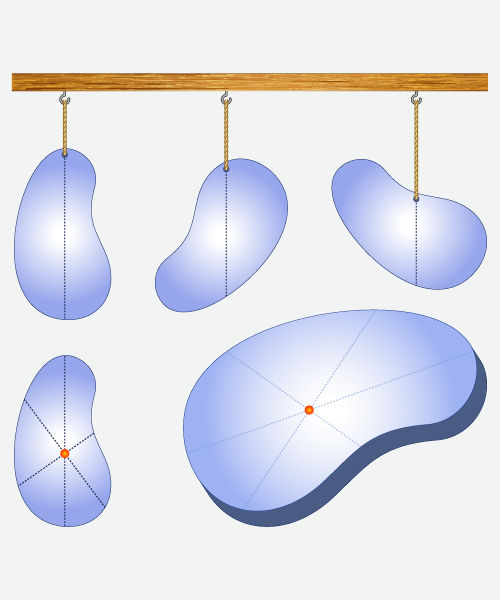
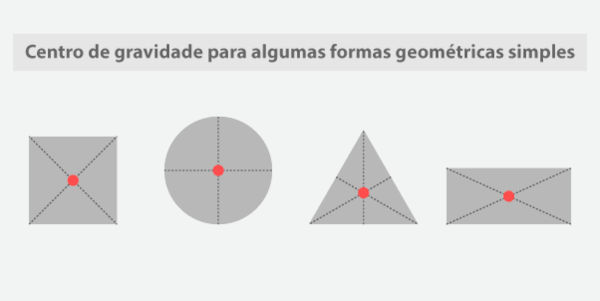
Separamos algumas figuras que indicam o centro de gravidade de formas geométricas simples, que podem ser obtidas por meio do experimento do equilíbrio:

Exercícios resolvidos sobre centro de gravidade

Questão 1

No eixo x, qual a posição do centro de gravidade do sistema constituído das seguintes partículas: partícula de massa m₁ = 1 kg na posição x₁ = 1 m; partícula de massa m₂ = 2 kg na posição x₂ = 2 m; partícula de massa m₃ = 3 kg na posição x₃ = 3 m; e partícula de massa m₄ = 4 kg na posição x₄ = 4 m.

A) 0

B) 1 m

C) 2 m

D) 3 m

E) 4 m

Resolução:

Alternativa D.

Usando a fórmula do centro de gravidade no eixo x:

\(x_{CG} = \frac{m_1 \cdot x_1 + m_2 \cdot x_2 + m_3 \cdot x_3 + m_4 \cdot x_4}{m_1 + m_2 + m_3 + m_4} = \frac{1 \cdot 1 + 2 \cdot 2 + 3 \cdot 3 + 4 \cdot 4}{1 + 2 + 3 + 4} = \frac{1 + 4 + 9 + 16}{10} = \frac{30}{10} = 3\ \text{m} \)

Questão 2

Um sistema é constituído por quatro partículas de massa m = 2 kg. A partícula 1 está posicionada no ponto (-1, 0), a partícula 2 está posicionada no ponto (0, 1), a partícula 3 está posicionada no ponto (1, 0), e a partícula 4 está posicionada no ponto (0, -1). Qual a posição do centro de gravidade do sistema?

A) (0, 0)

B) (-1, 0)

C) (0, -1)

D) (1, 0)

E) (0, 1)

Resolução:

Alternativa A.

Usando a fórmula do centro de gravidade no eixo x:

\(x_{CG} = \frac{2 \cdot (-1) + 2 \cdot 0 + 2 \cdot 1 + 2 \cdot 0}{2 + 2 + 2 + 2} = \frac{-2 + 0 + 2 + 0}{8} = \frac{0}{8} = 0 \)

Usando a fórmula do centro de gravidade no eixo y:

\(y_{CG} = \frac{2 \cdot 0 + 2 \cdot 1 + 2 \cdot 0 + 2 \cdot (-1)}{2 + 2 + 2 + 2} = \frac{0 + 2 + 0 - 2}{8} = \frac{0}{8} = 0 \)

Crédito de imagem

MikeRun / Wikimedia Commons (reprodução)

Fontes

CARRON, Wilson; GUIMARÃES, Osvaldo. As faces da física (vol. único). 1. ed. Moderna, 1997.

HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos da Física: Gravitação, ondas e termodinâmica (vol. 2). 9 ed. Rio de Janeiro, RJ: LTC, 2012.

NUSSENZVEIG, Herch Moysés. Curso de física básica: Mecânica (vol. 1). 5 ed. São Paulo: Editora Blucher, 2015.