Divisão de polinômios

Divisão de polinômios possui diferentes métodos de resolução. Vamos apresentar três métodos para essa divisão: o método de Descartes (coeficientes a determinar), o método da chave e o dispositivo prático de Briot-Ruffini.

Leia mais: Equação polinomial: forma e como resolver

Tópicos deste artigo

• 1 - Divisão de polinômios
• 2 - Regras da divisão de polinômios
  • Método dos coeficientes a determinar — método de Descartes
  • Exemplo
  • Método da chave
  • Dispositivo prático de Briot-Ruffini
• 3 - Exercícios resolvidos

Divisão de polinômios

Ao dividir um polinômio P (x) por um polinômio D (x) não nulo, em que o grau de P é maior que D (_P > _D), quer dizer que devemos encontrar um polinômio Q (x) e R (x), de modo que:

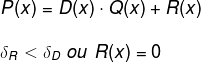
Note que esse processo é equivalente a escrever:

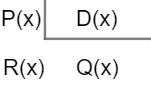
P (x) → dividendo

D (x) → divisor

Q (x) → quociente

R (x) → resto

Das propriedades da potenciação, temos que o grau do quociente é igual à diferença entre os graus do dividendo e divisor.

_{Q = P – D}

Ainda, quando o resto da divisão entre P (x) e D (x) é igual a zero, dizemos que P (x) é divisível por D (x).

Regras da divisão de polinômios

• Método dos coeficientes a determinar — método de Descartes

Para realizar a divisão entre os polinômios P (x) e D (x), com grau de P maior que o grau de D, seguimos os passos:

Passo 1 - Determinar o grau do polinômio quociente Q (x);

Passo 2 - Tomar o maior grau possível para o resto da divisão R (X) (Lembre-se: R (x) = 0 ou _R < _D);

Passo 3 - Escrever os polinômios Q e R com coeficientes literais, de forma que P (x) = D (x) · Q (x) + R (x).

• Exemplo

Sabendo-se que P (x) = 4x³ – x² + 2 e que D (x) = x² + 1, determina-se o polinômio quociente e o resto.

O grau do quociente é 1, pois:

_Q = _{P – D}

_Q = 3 – 2

_Q = 1

Assim no polinômio Q (x) = a·x +b, o resto R (x) é um polinômio cujo maior grau pode ser 1, logo: R (x) = c ·x +d. Substituindo os dados na condição do passo 3, temos:

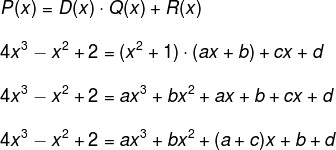
Comparando os coeficientes dos polinômios, temos:

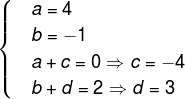
Logo, o polinômio Q (x) = 4x-1 e R (x) = -4x + 3.

• Método da chave

Consiste em realizar a divisão entre polinômios seguindo a mesma ideia da divisão entre dois números, o chamado algoritmo da divisão. Veja o exemplo a seguir.

Novamente vamos considerar os polinômios P (x) = 4x³ – x² + 2 e D (x) = x² + 1, e agora vamos dividi-los utilizando o método da chave.

Passo 1 - Completar o polinômio dividendo com coeficientes nulos, caso necessário.

P (x) = 4x³ – x² + 0x + 2

Passo 2 - Dividir o primeiro termo do dividendo pelo primeiro termo do divisor e, em seguida, multiplicar o quociente por todo divisor. Veja:

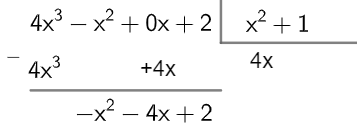
Passo 3 - Dividir o resto do passo 2 pelo quociente e repetir esse processo até que o grau do resto seja menor que o grau do quociente.

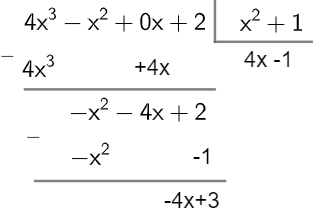
Logo, Q (x) = 4x-1 e R (x) = -4x +3.

Acesse também: Adição, subtração e multiplicação de polinômios

• Dispositivo prático de Briot-Ruffini

Utilizado para dividir polinômios por binômios.

Vamos considerar os polinômios: P (x) = 4x³ + 3 e D (x) = 2x + 1.

Esse método consiste em desenhar dois segmentos, um horizontal e outro vertical, e nesses segmentos colocamos o coeficiente do dividendo e a raiz do polinômio divisor, além disso, repete-se o primeiro coeficiente. Veja:

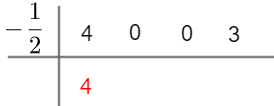
Perceba que o menor meio é a raiz do divisor e que o primeiro coeficiente foi divido.

Agora, devemos multiplicar a raiz do divisor pelo termo repetido e somá-lo ao próximo, veja:

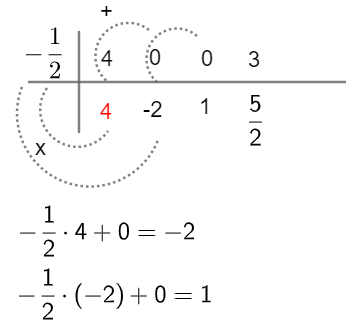
O último número encontrado no dispositivo prático é o resto, e os demais são os coeficientes do polinômio quociente. Devemos dividir esses números pelo primeiro coeficiente do divisor, nesse caso por 2. Assim:

Para saber mais sobre esse método de divisão de polinômios, acesse: divisão de polinômios utilizando o dispositivo de Briot-Ruffini.

Exercícios resolvidos

Questão1 (UFMG) O polinômio P (x) = 3x⁵ - 3x⁴ -2x³ + mx² é divisível por D (x) = 3x² - 2x. O valor de m é:

Solução

Como o polinômio P é divisível por D, então podemos aplicar o algoritmo da divisão. Assim,

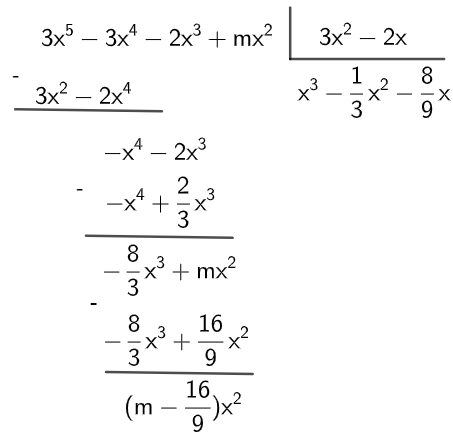
Como foi dado que os polinômios são divisíveis, então o resto é igual a zero. Logo, 

Por Robson Luiz
Professor de Matemática