Afinal, o que é meia-vida? A meia-vida é uma constante definida como o tempo necessário para que a atividade de uma amostra radioativa decaia pela metade. Nesse tempo, é possível dizer que as quantidades de desintegrações, de número de mols e de massa também caem pela metade. Cada radioisótopo possui um tempo específico de meia-vida, o que é determinado experimentalmente.
A meia-vida possui uma fórmula para seu cálculo, embora seja possível utilizar a meia-vida pelo seu conceito, projetando a queda do radioisótopo a cada meia-vida passada. A meia-vida é muito utilizada para datação arqueológica, destacando-se a datação via carbono-14, que permite predizer a quantidade de tempo passado desde a morte de um organismo.
Leia também: Afinal, o que é radioatividade?
Tópicos deste artigo
- 1 - Resumo sobre meia-vida
- 2 - Afinal, o que é meia-vida?
- 3 - Fórmula da meia-vida
- 4 - Como calcular a meia-vida?
- 5 - Para que serve a meia-vida?
- 6 - Exercícios resolvidos sobre meia-vida
Resumo sobre meia-vida
- A meia-vida é o intervalo de tempo necessário para que a atividade, a massa, o número de mols ou a quantidade de desintegrações de uma amostra radioativa reduza-se à metade do valor inicial.
- Cada radioisótopo apresenta um tempo de meia-vida característico e exclusivo, sendo esse valor determinado por meio de medições experimentais.
- Embora exista uma fórmula para seu cálculo, o conceito de meia-vida permite projetar a redução do radioisótopo a cada período transcorrido.
- A meia-vida é uma ferramenta essencial e amplamente empregada em métodos de datação arqueológica de materiais orgânicos e inorgânicos.
- O método de datação que utiliza o carbono-14 é notável, pois permite estimar o tempo decorrido desde a morte de organismos vivos.
Afinal, o que é meia-vida?
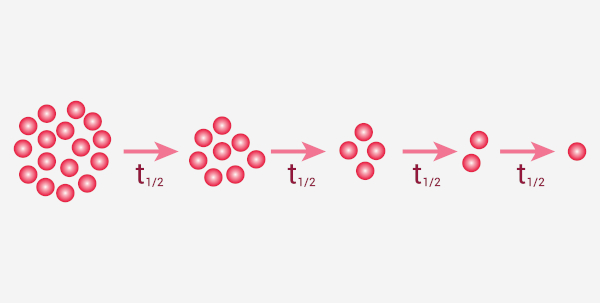
A meia-vida é o tempo necessário para que, em um processo de decaimento radioativo, a quantidade da espécie radioativa (e, assim sendo, a sua atividade) caia pela metade. A meia-vida é comumente representada por “t1/2”, sendo um parâmetro importante para átomos radioativos.
A tabela a seguir traz alguns tempos de meia-vida para alguns isótopos radioativos.
|
Isótopo |
t1/2 |
|
14C |
5715 anos |
|
24Na |
14,96 horas |
|
40K |
1,248 x 109 anos |
|
131I |
8,021 dias |
|
137Cs |
30,2 anos |
|
235U |
7,03 x 108 anos |
|
242Pu |
3,75 x 105 anos |
|
294Og |
0,9 x 10−3 segundos |
Fórmula da meia-vida
A meia-vida pode ser aplicada da seguinte forma:
\(N = \frac{N_0}{2^x}\)
Na fórmula, “x” é igual a:
\(x = \frac{p}{t_{1/2}}\)
Dessa forma, entendemos os seguintes parâmetros para a equação:
- N → quantidade final da amostra radioativa.
- N0 → quantidade inicial da amostra radioativa.
- P → período (intervalo de tempo) avaliado.
- t1/2 → tempo de meia-vida da espécie.
Como calcular a meia-vida?
A meia-vida pode ser calculada pela fórmula ou por um método simples, utilizando-se seu conceito, em que se vai decrescendo a quantidade radioativa pela metade até chegar-se ao ponto de interesse. Vejamos um caso em que utilizaremos os cálculos de meia-vida das duas formas anteriormente citadas.
|
O isótopo césio-137 é muito ligado à história brasileira, por conta do acidente radiológico da cidade de Goiânia, capital de Goiás, no ano de 1987. Especialistas afirmam que serão 180 anos para que os rejeitos do acidente apresentem níveis seguros do césio-137. Sabendo que o tempo de meia-vida desse radioisótopo é de 30 anos, indique a porcentagem remanescente de césio-137 após o período indicado pelos especialistas. |
- Método 1: Pela fórmula
Se o tempo de meia-vida do césio-137 é de 30 anos e o período avaliado é de 180 anos, portanto, o índice x, que corresponde ao número de meias-vidas é:
\(x = \frac{p}{t_{1/2}} = \frac{180}{30} = 6 \)
Substituindo o valor de x na fórmula da meia-vida, temos que:
\(N = \frac{N_0}{2^x} \)
\(N = \frac{100\%}{2^6} \cong 1,5\% \)
Portanto, após 180 anos, apenas cerca de 1,5% de césio-137 do acidente ainda existirá.
- Método 2: Pelo conceito de meia-vida
Se a meia-vida do césio-137 é de 30 anos, podemos imaginar que, após 30 anos, apenas 50% da sua quantidade inicial ainda existe.
Passados mais 30 anos, agora totalizando 60 anos, a quantidade cai pela metade, e, portanto, restam 25% do isótopo em questão.
Passados mais 30 anos, agora totalizando 90 anos, a quantidade cai pela metade, e, portanto, restam 12,5% do isótopo em questão.
Passados mais 30 anos, agora totalizando 120 anos, a quantidade cai pela metade, e, portanto, restam 6,25% do isótopo em questão.
Passados mais 30 anos, agora totalizando 150 anos, a quantidade cai pela metade, e, portanto, restam 3,125% do isótopo em questão.
Passados mais 30 anos, enfim chegando aos 180 anos, a quantidade cai pela metade, e, portanto, restam 1,5625% do isótopo em questão, ou seja, aproximadamente 1,5%.
Para que serve a meia-vida?
A meia-vida, sendo uma constante, é amplamente utilizada para fins de datação arqueológica. Nesse caso, mede-se a atividade dos isótopos radioativos nos artefatos arqueológicos que estão sendo datados. Dentre os isótopos radioativos mais comumente usados, podemos citar o urânio-238, o potássio-40, o trítio (3H) e o mais conhecido de todos, o carbono-14, cuja técnica é conhecida como datação por carbono radioativo.
Nessa técnica, utiliza-se o decaimento beta (β) do radioisótopo, cujo tempo de meia-vida é de cerca de 5700 anos.
\(^{14}_{6}\mathrm{C} \rightarrow ^{0}_{-1}\beta + ^{14}_{7}\mathrm{N} \)
No caso, sabe-se que o carbono-12 é o principal isótopo de carbono, porém, uma pequena quantidade de carbono-14 também está presente em seres vivos. Os átomos de carbono-14 são produzidos na atmosfera, mediante bombardeamento de nêutrons aos átomos de nitrogênio-14:
\(^{14}_{7}\mathrm{N} + ^{1}_{0}\mathrm{n} \rightarrow ^{14}_{6}\mathrm{C} + ^{1}_{1}\mathrm{p}\)
A velocidade de produção do carbono-14 é praticamente a mesma ao longo dos anos, e, dessa forma, a proporção entre o carbono-14 e o carbono-12 na atmosfera é praticamente constante com o tempo. Os organismos vivos, por meio da fotossíntese ou da digestão, incorporam o carbono-14 através do 14CO2.
O carbono-14 é excretado por meio de processos normais, como a respiração e, claro, mediante decaimento a uma velocidade determinada. Com isso, entende-se que todos os seres vivos possuem uma razão fixa entre o carbono-14 e o carbono-12 (cerca de 1 átomo de carbono-14 para cada 1012 átomos de carbono-12).
Ao morrer, o organismo não mais incorpora carbono, contudo, os átomos de carbono-14 presentes no organismo morto continuam a se desintegrar com uma meia-vida constante. Com isso, a razão entre o carbono-14 e o carbono-12 decresce e, assim, tal valor pode ser utilizado para estimar o tempo decorrido desde a morte.

A técnica foi desenvolvida nos anos 1940, por Willard Libby. À época, a proporção de carbono-14 era determinada a partir do monitoramento da radiação β oriunda do CO2 obtido via combustão da amostra. Atualmente, a técnica foi aprimorada, permitindo a utilização de poucos miligramas da amostra, em que os átomos de carbono são convertidos ao íon C− por meio de bombardeamento com átomos de césio. Esses íons de carbono são, então, acelerados por campos elétricos, e os isótopos são separados e contados em um espectrômetro de massas.
Acesse também: Você sabe o que é a lei da radioatividade?
Exercícios resolvidos sobre meia-vida
Questão 1
(UEA) O radioisótopo tálio-201 é usado como contraste injetável em exames de imagem que avaliam o fluxo sanguíneo e a função cardíaca. O gráfico representa a curva de decaimento radioativo desse radioisótopo.
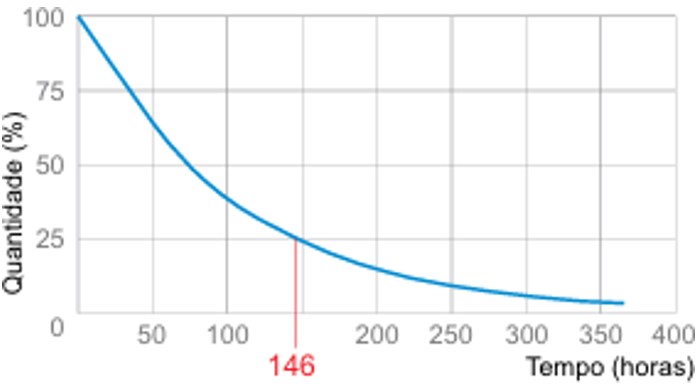
A meia-vida do tálio-201 é
A) 73 horas.
B) 146 horas.
C) 50 horas.
D) 25 horas.
E) 100 horas.
Resolução:
Alternativa A.
Pelo gráfico, é possível perceber que o tálio-201 demorou 146 horas para chegar a 25% da sua quantidade inicial. Dessa forma, é possível perceber que foram passados dois tempos de meia-vida: de 100% para 50% e, depois, de 50% para 25%. Como o tempo de meia-vida é constante, podemos dizer, portanto, que o tempo de meia-vida para o tálio-201 é igual à metade de 146 horas (o tempo decorrido, dividido pelo número de meias-vidas), que corresponde a 73 horas.
Também é possível determinar o valor da meia-vida pela fórmula:
\(N = \frac{N_0}{2^x} \)
\(25\% = \frac{100\%}{2^x}\)
\(2^x = \frac{100\%}{25\%} = 4 = 2^2 \)
Assim, concluímos que x (número de meias-vidas) é igual a 2. Portanto, sendo p (o tempo decorrido) igual a 146 horas, temos que:
x = p/t1/2
t1/2 = 146/2
t1/2 = 73 horas
Questão 2
(Uece) O lutécio-177 é um radioisótopo utilizado no tratamento de certos tipos de câncer, como os tumores neuroendócrinos. Para o estudo de um medicamento utilizado nesse tipo de terapia, foi preparada uma amostra contendo 200 mg desse radioisótopo, cujo tempo de meia-vida é de aproximadamente 6 dias.
O intervalo de tempo, em dias, necessário para que a massa de lutécio-177 na amostra seja reduzida a 25 mg é, aproximadamente,
A) 6.
B) 12.
C) 18.
D) 24.
Resolução:
Alternativa C.
Inicialmente, a amostra do lutécio-177 é de 200 mg. Portanto, fazendo-se a análise com seu tempo de meia-vida (6 dias):
- Após 6 dias, 200 mg decaíram para 100 mg.
- Após mais 6 dias, totalizando 12 dias, 100 mg decaíram para 50 mg.
- Após mais 6 dias, totalizando 18 dias, 50 mg decaíram para 25 mg.
Portanto, o tempo necessário para a redução de 200 mg de lutécio-177 para 25 mg do mesmo radioisótopo é de 18 dias.
Fontes
DO CANTO, E. L.; LEITE, L. L. C.; CANTO, L. C. Química – na abordagem do cotidiano. 1. ed. São Paulo: Moderna, 2021.
ATKINS, P.; JONES, L.; LAVERMAN, L. Princípios de Química: Questionando a vida e o meio ambiente. 7. ed. Porto Alegre: Bookman, 2018.
HAYNES, W. M. (ed.) CRC Handbook of Chemistry and Physics. 95a ed. CRC Press: 2014.

