Gráfico de uma função

O gráfico de uma função é uma representação que nos permite analisar o comportamento da função, mostrando qual é a relação existente entre os valores do domínio e do contradomínio da função. Cada tipo de função possui um gráfico específico. Por exemplo, o gráfico de uma função polinomial de 1º grau é sempre uma reta; já o gráfico de uma função polinomial de 2º grau é sempre uma parábola.

Para fazer a representação gráfica da função, é necessário conhecer a imagem para alguns valores do domínio. Com base na representação desses pontos de domínio e imagem no plano cartesiano, torna-se possível fazer a representação do gráfico da função.

Leia também: Afinal, o que é o plano cartesiano?

Resumo sobre gráfico de uma função

• O gráfico da função é a representação da relação entre o domínio e a imagem no plano cartesiano.
• O gráfico da função nos permite analisar características importantes da função.
• Cada tipo de função possui um comportamento gráfico específico. Por exemplo, funções de 1º grau possuem gráficos que são sempre retas; já para as de 2º grau, o gráfico é sempre uma parábola.
• Para fazer a representação gráfica, é necessário conhecer a imagem para alguns valores no domínio.

Tipos de gráficos de funções

O gráfico da função depende diretamente da lei de formação da função. Cada função possui um gráfico específico cuja representação pode ser feita no plano cartesiano. As funções polinomiais de 1º grau, por exemplo, possuem gráficos iguais a uma reta. Essa reta pode se posicionar de diferentes maneiras no plano cartesiano a depender da lei de formação da função.

Gráfico de uma função polinomial de 1º grau

A função polinomial de 1º grau possui lei de formação f(x) = ax + b. Veja, a seguir, a representação do gráfico de um caso particular de função afim, a função f(x) = -x.

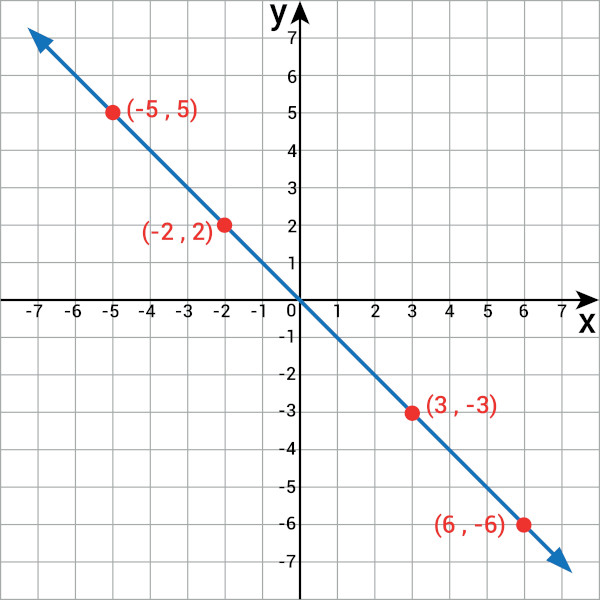
Leis de formação diferentes geram gráficos diferentes, mas o gráfico de uma função polinomial de 1º grau é sempre uma reta.

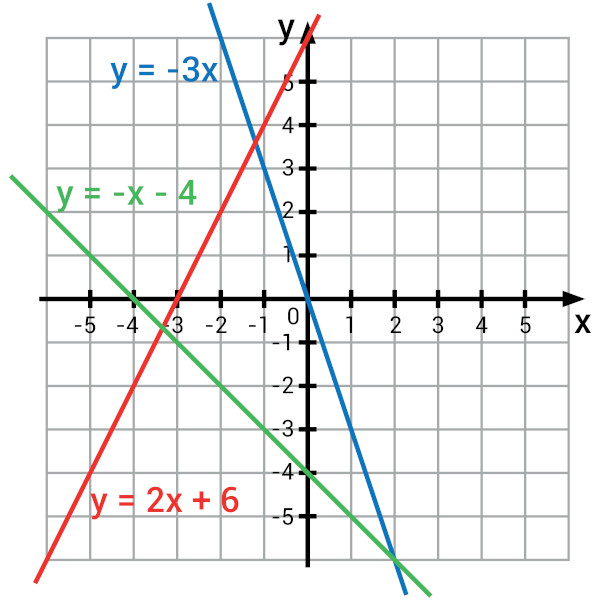
Gráfico de uma função polinomial de 2º grau

O comportamento do gráfico da função polinomial de 2º grau é diferente do comportamento do gráfico da função de 1º grau. O gráfico da função polinomial de 2º grau é sempre uma parábola. Podemos ter diferentes parábolas em diferentes posições no plano cartesiano, dependendo da lei de formação da função. A função de 2º grau, conhecida também como função quadrática, possui lei de formação f(x) = ax² + bx + c.

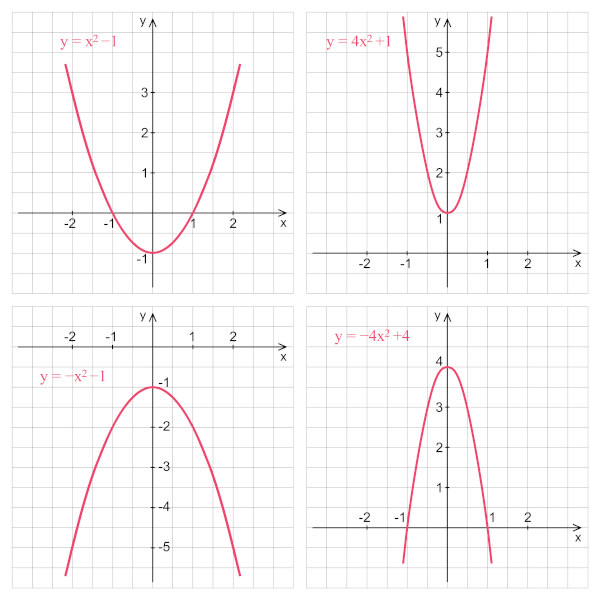
Gráfico de uma função exponencial

A função exponencial tem um crescimento mais rápido que o da função polinomial de 1ºgrau porque a variável está no expoente. A lei de formação da função exponencial é f(x) = a^x.

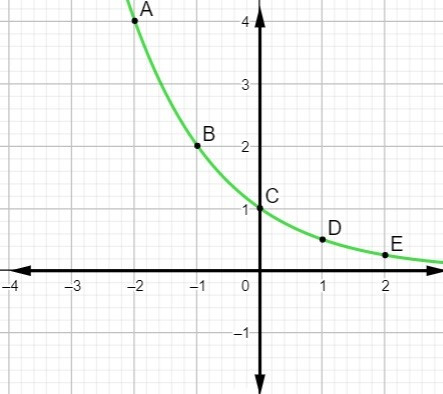
Outros tipos de gráficos de funções

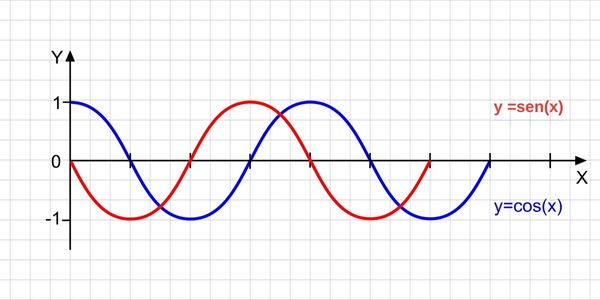
Existem vários outros tipos de função, sendo assim, podemos ver vários outros tipos de gráficos. Temos, por exemplo: o gráfico da função modular; o gráfico das funções trigonométricas, como a função seno, a função cosseno e a função tangente; e o gráfico de uma função polinomial de 3º grau, 4º grau, 5º grau. Sabemos que existem uma infinitude de funções e cada uma delas pode ser representada graficamente.

Saiba mais: O que é uma função injetora?

Elementos do gráfico de uma função

Cada tipo de função possui elementos específicos. De forma geral, podemos falar sobre o zero da função e o crescimento ou decrescimento da função.

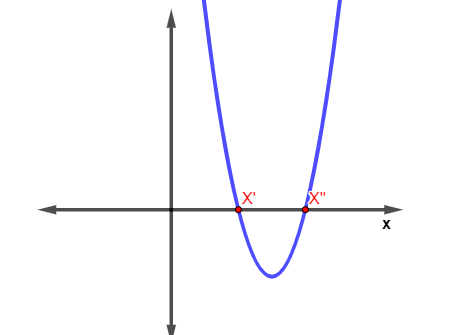
→ Zeros da função

Analisando o gráfico da função, os pontos em que o gráfico da função corta o eixo x são conhecidos como zero da função ou raízes da função.

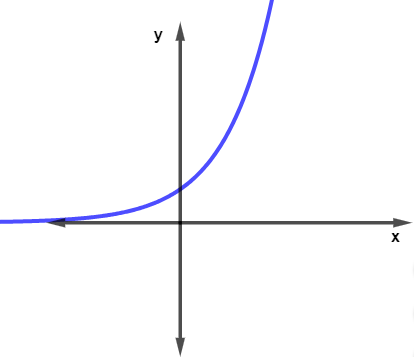
→ Crescimento e decrescimento da função

• Função crescente: uma função ou parte da função é dita crescente se, à medida que o valor de x aumenta, o valor de y também aumenta.

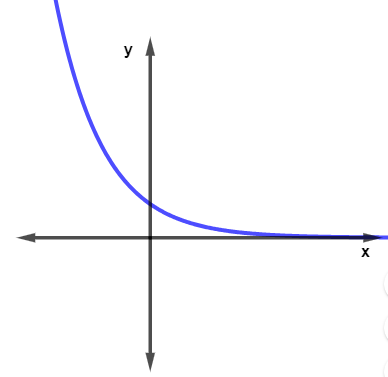
• Função decrescente: a função é decrescente se, à medida que o valor de x aumenta, o valor de y diminui.

Como construir o gráfico de uma função

→ Como fazer o gráfico de uma função polinomial de 1º grau

Para construir o gráfico de uma função de 1º grau, basta conhecer dois pontos dessa função. Para isso, atribuiremos alguns valores para x e encontraremos o correspondente para y. Posteriormente, marcaremos esses dois pontos no plano cartesiano e traçaremos a reta que passa por eles.

Exemplo: f(x) = 2x + 1

• 1º passo: atribuir valores para x.

Primeiro vamos atribuir dois valores diferentes parar x e encontrar o correspondente em y. Lembre-se de que esse valor de x pode ser à sua escolha, e o recomendado é escolher valores que sejam menores e mais fáceis de calcular, por exemplo, x = 1.

f(1) = 2 ⋅ 1 + 1 = 2 + 1 = 3

Então, o ponto (1, 3) pertence à função.

Faremos agora x = 0.

f(0) = 2 ⋅ 0 + 1 = 0 + 1 = 1

Então, o ponto (0, 1) pertence ao gráfico.

• 2º passo: marcar os pontos no plano cartesiano.

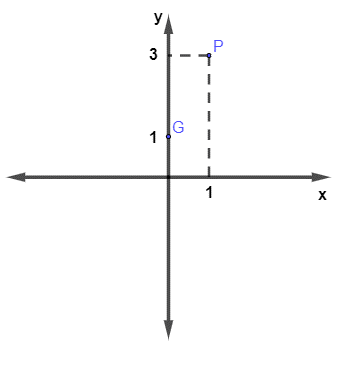
• 3º passo: traçar a reta que passa pelos dois pontos.

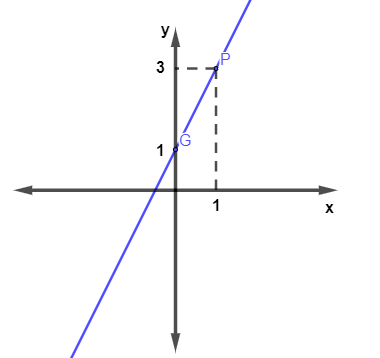
→ Como fazer o gráfico de uma função polinomial de 2º grau

Para realizar o esboço do gráfico de uma função, é necessário encontrar os zeros, o seu vértice e o ponto em que a função toca o eixo y.

Exemplo:

f(x) = x² – 6x + 8

• 1º passo: zeros da função.

Para encontrar o zero da função quadrática, faremos:

x² – 6x + 8 = 0

Na função quadrática, temos que:

a = 1, b = -6 e c = 8

\(\mathrm{\Delta}=b^2-4ac\)

\(\mathrm{\Delta}=\left(-6\right)^2-4\cdot1\cdot8\)

\(\mathrm{\Delta}=36-32\)

\(\mathrm{\Delta}=4\)

\(x=\frac{-b\pm\sqrt{\Delta}}{2a}\)

\(x=\frac{-\left(-6\right)\pm\sqrt4}{2\cdot1}\)

\(x=\frac{6\pm2}{2}\)

\(x_1=\frac{6+2}{2}=\frac{8}{2}=4\)

\(x_2=\frac{6-2}{2}=\frac{4}{2}=2\)

Então, os pontos (2, 0) e (4, 0) pertencem à função.

• 2º passo: calcular o vértice.

Para calcular o vértice, utilizamos as fórmulas:

\(x_v=\frac{-b}{2a}\)

\(y_v=\frac{-\mathrm{\Delta}}{4a}\)

Substituindo os valores da função:

\(x_v=\frac{--6}{2\cdot1}=-\left(-3\right)=3\)

\(y_v=\frac{-4}{4\cdot1}=-1\)

Então, o vértice é o ponto (3, -1).

• 3º passo: calcular f(0).

f(x) = x² – 6x + 8

f(0) = 0² – 6 ⋅0 + 8

f(0) = 8

Logo, o ponto (0, 8) pertence ao gráfico.

• 4º passo: marcar os pontos e traçar a parábola.

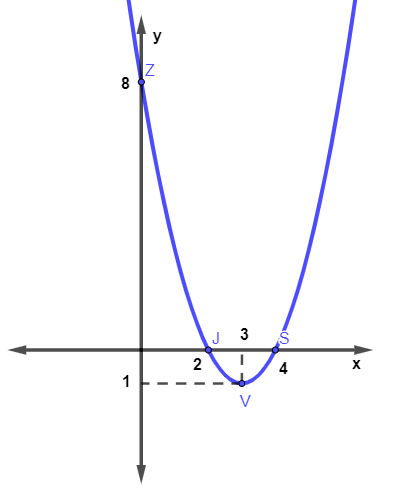
→ Como fazer o gráfico de uma função exponencial

Assim como na função afim, na função exponencial atribuiremos alguns valores para x e encontraremos o valor de y.

Exemplo:

f(x) = 3^x

Calcularemos cinco pontos, sendo eles f(-2), f(-1), f(0), f(1) e f(2).

\(f\left(-2\right)=3^{-2}=\frac{1}{9}\)

\(f\left(-1\right)=3^{-1}=\frac{1}{3}\)

\(f\left(0\right)=3^0=1\)

\(f\left(1\right)=3^1=3\)

\(f\left(2\right)=3^2=9\)

Assim, os pontos são:

\(\left(-2,\ \frac{1}{9}\right),\left(-1,\ \frac{1}{3}\right),\left(0,\ 1\right),\left(1,\ 3\right)\ e\ \left(2,\ 9\right)\)

Marcaremos esses pontos no plano cartesiano e traçaremos a curva que passa por eles:

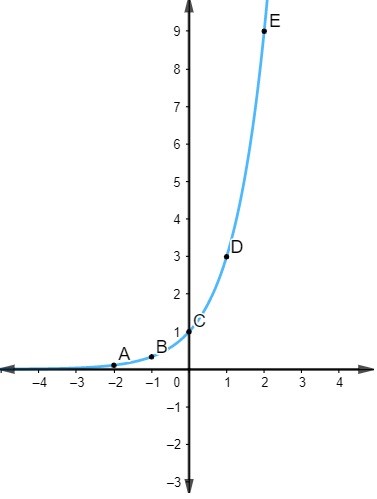
Exercícios resolvidos sobre gráfico de uma função

Questão 1

Analise o gráfico da função a seguir:

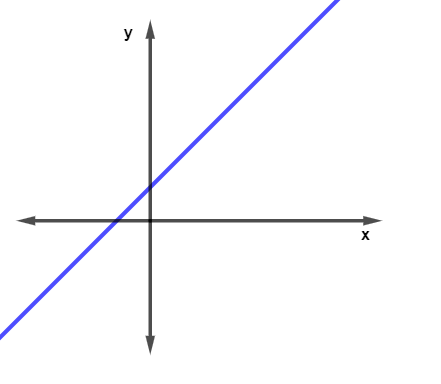
Com base no gráfico da função acima, podemos afirmar que:

I – Essa função é uma função polinomial de 2º grau.

II – O gráfico dessa função é crescente.

III – Essa função possui um único zero.

Marque a alternativa correta:

A) Somente a afirmativa I é falsa.

B) Somente a afirmativa II é falsa.

C) Somente a afirmativa III é falsa.

E) Todas as afirmativas são verdadeiras.

Resolução:

Alternativa A

I – Essa função é uma função polinomial de 2º grau. (falsa)

O gráfico é uma reta, portanto, é uma função de 1º grau.

II – O gráfico dessa função é crescente. (verdadeira)

Note que, à medida que x aumenta, o y também aumenta.

III – Essa função possui um único zero. (verdadeira)

A reta corta o eixo x em um único ponto.

Questão 2

Sobre o gráfico da função polinomial de 2º grau, marque a alternativa correta.

A) O gráfico da função polinomial de 2º grau é sempre crescente.

B) O gráfico da função polinomial de 2º grau é sempre decrescente.

C) O gráfico da função polinomial de 2º grau pode ser uma reta.

D) O gráfico da função polinomial de 2º grau é constante.

E) O gráfico da função polinomial de 2º grau tem parte crescente e parte decrescente.

Resolução:

Alternativa E

Como o gráfico da função polinomial é uma parábola, podemos observar que ele possui uma parte crescente e uma parte decrescente.

Fontes

LIMA, E. L. et al. A Matemática do Ensino Médio. 9. ed. Rio de Janeiro: SBM, 2006. 3 v. (Coleção do professor de Matemática).