Proporção

A proporção é definida como a igualdade entre duas razões, caso essa igualdade seja verdadeira, então dizemos que os números que foram as razões na ordem dada são proporcionais.

O estudo das proporções é essencial para o desenvolvimento matemático, pois elas possibilitam-nos relacionar grandezas, assim resolvendo problemas do nosso cotidiano. São exemplos de proporções: escala de um mapa, velocidade média de um móvel, e densidade de uma solução.

Leia também: Problemas envolvendo números fracionários

O que é razão e proporção?

A razão entre dois números é o quociente entre eles na ordem em que são dados. Sejam a e b dois números racionais, em que b é diferente de 0, a razão entre a e b é dada por:

Quando se tem duas razões e ambas estão sendo comparadas por uma igualdade, então temos uma proporção. Caso a igualdade seja verdadeira, então os números serão proporcionais, caso contrário, então eles não serão proporcionais.

Os números racionais a, b, c e d são proporcionais se, e somente se, a igualdade a seguir for verdadeira.

De maneira equivalente, podemos dizer que a igualdade será verdadeira somente quando a multiplicação cruzada for verdadeira.

Propriedades da proporção

Considere a seguinte proporção entre os números a, b, c e d:

Então as seguintes propriedades são válidas:

Propriedade 1 – O produto dos meios é igual ao produto dos extremos (multiplicação cruzada).

Propriedade 2 – A razão entre a soma (ou diferença) dos dois primeiros termos e o primeiro termo é igual à razão entre a soma (ou diferença) dos dois últimos termos e o terceiro termo.

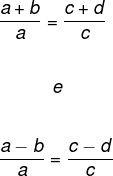
Leia também: Propriedades da proporção – quais são e como calcular?

Como calcular proporções

Para verificar ou calcular se, de fato, os números são proporcionais, basta aplicar a primeira propriedade, caso a igualdade seja verdadeira, então os números são proporcionais. Veja os exemplos:

Exemplo 1

Verifique se os números 15, 30, 45 e 90 são proporcionais.

Devemos, nessa ordem, montar as razões e, em seguida, realizar a multiplicação cruzada.

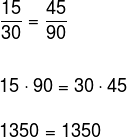
Observe que a igualdade é verdadeira, assim os números formam, nessa ordem, uma proporção.

Exemplo 2

Sabe-se que os números 2, 4, x e 32 são proporcionais. Determine o valor de x.

Por hipótese, temos que os números, na ordem que foram apresentados, são proporcionais, logo, podemos igualar as razões entre eles e aplicar a propriedade 1, veja:

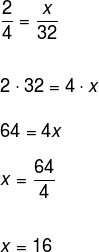
Grandezas direta e inversamente proporcionais

Grandeza, em matemática, é tudo aquilo que é possível medir ou mensurar, por exemplo, quantidade, distância, massa, volume etc. As grandezas podem ser diretamente proporcionais (GDP) ou inversamente proporcionais (GIP), vejamos a diferença entre elas:

Grandezas diretamente proporcionais

Dizemos que duas ou mais grandezas são diretamente proporcionais se a razão dos valores da primeira grandeza é igual à dos valores da segunda grandeza, e assim sucessivamente. Por exemplo, a grandeza massa é proporcional ao peso de um objeto, veja na tabela:

Observe que a razão entre as grandezas é sempre igual:

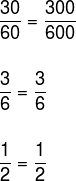
O mesmo vai acontecer se realizarmos a razão entre os demais valores.

Outra maneira de saber se duas ou mais grandezas são diretamente proporcionais é verificando o crescimento ou decrescimento de ambas. Por exemplo, se uma grandeza aumenta, a outra também deverá aumentar, caso elas sejam diretamente proporcionais. Vejamos o exemplo:

Na tabela de massa x peso, veja que quanto maior é a massa do objeto (↑), maior será o peso dele (↑), logo, as grandezas são diretamente proporcionais.

Exemplo

Os números x, t e 2 são diretamente proporcionais aos números 5, 6 e 10. Determine os valores de x e t.

Como o exemplo afirmou-nos que os números são diretamente proporcionais, então a razão entre eles é igual, assim:

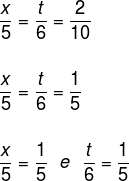
Multiplicando cruzado cada uma das igualdades, temos:

5x = 5

x = 1

e

5t = 6

t = 6 ÷ 5

t = 1,2

Portanto, x = 1 e t = 1,2.

Grandezas inversamente proporcionais

Duas ou mais grandezas serão inversamente proporcionais se a razão entre os valores da primeira for igual ao inverso da razão dos valores da segunda. Podemos interpretar isso de outra maneira, se uma grandeza cresce (↑) e a outra grandeza decresce (↓), então elas são inversamente proporcionais. Veja o exemplo:

As grandezas velocidade e tempo são inversamente proporcionais.

Observe que quanto maior é a velocidade de determinada viagem (↑), menor será o tempo dessa viagem (↓). Veja também que se pegarmos a razão entre dois valores da primeira grandeza e o inverso da razão de dois valores da segunda grandeza, a igualdade será verdadeira.

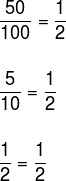
Exemplo

Divida o número 120 em partes inversamente proporcionais aos números 4 e 6.

Como queremos dividir o número 120 em duas partes e desconhecemo-las, vamos chamá-las de a e 120 – a. Pela definição de inversamente proporcional, a razão entre os primeiros valores é igual ao inverso da razão dos dois últimos valores. Assim:

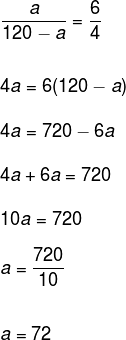
Como a outra parte é 120 – a, então:

120 – a

120 – 72

48

Portanto, ao dividirmos o número 120 em partes inversamente proporcionais aos números 4 e 6, obtemos 72 e 48.

Exercício resolvido

Questão 1 – (Fuvest) Na tabela a seguir, y é inversamente proporcional ao quadrado de x. Calcule os valores de p e m.

Resolução

Observe que o enunciado afirma que os valores de y são inversamente proporcionais aos do quadrado de x, ou seja, a razão entre os valores de y será igual ao inverso dos valores de x elevado ao quadrado.

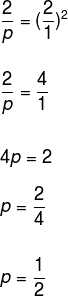
Usando a mesma lógica, vamos determinar o valor de m.

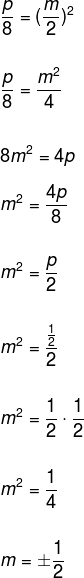
Por Robson Luiz
Professor de Matemática