Triângulo isósceles
Triângulo isósceles possui dois lados congruentes, e, por isso, ele tem propriedades específicas e importantes de serem aprendidas.
Triângulo isósceles é aquele que possui dois lados congruentes. Classificamos os triângulos de acordo com as suas características, e uma das classificações leva em consideração a medida dos seus lados. Nesse caso, além do tipo isósceles, existem mais dois: o escaleno, triângulo que possui todos os lados com medidas distintas; e o equilátero, triângulo que possui todos os lados congruentes.
No triângulo isósceles, os lados congruentes são conhecidos como oblíquos, e o outro lado é conhecido como base. O triângulo isósceles possui propriedades específicas, com a sua altura sendo a mediana da base e a bissetriz do ângulo, além disso, os ângulos da base são sempre congruentes. Para calcular área e perímetro de um triângulo isósceles, utilizamos a fórmula para área de um triângulo qualquer e o perímetro continua sendo a soma de todos os lados.
Resumo sobre triângulo isósceles
-
É aquele que possui dois lados congruentes (com a mesma medida).
-
Nele, os ângulos da base são sempre congruentes.
-
Sua altura é também a sua mediana.
Videoaula sobre triângulo isósceles
Triângulo isósceles
O triângulo é um polígono que possui muita importância no dia a dia, sendo amplamente estudado. Ele possui três lados e pode ser classificado como isósceles quando possui dois lados congruentes, ou seja, quando há dois lados com a mesma medida.
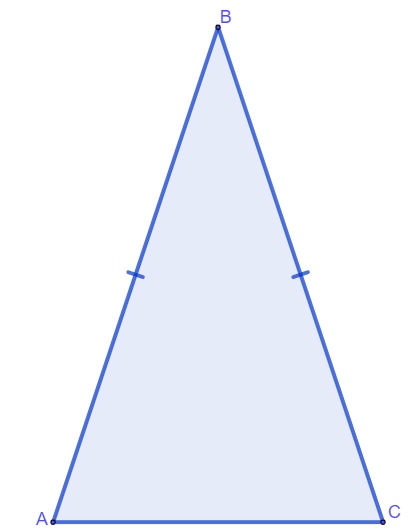
Nesse triângulo, os lados AB e BC possuem a mesma medida, o que faz com que ele seja isósceles, além disso, em um triângulo isósceles, o lado não congruente é conhecido como base, que, no caso, está sendo representada pelo lado AC.
Propriedades do triângulo isósceles
O triângulo isósceles possui duas propriedades muito úteis para resolução de problemas envolvendo esse tipo de figura.
1ª propriedade: em um triângulo isósceles, os ângulos da base são sempre congruentes.
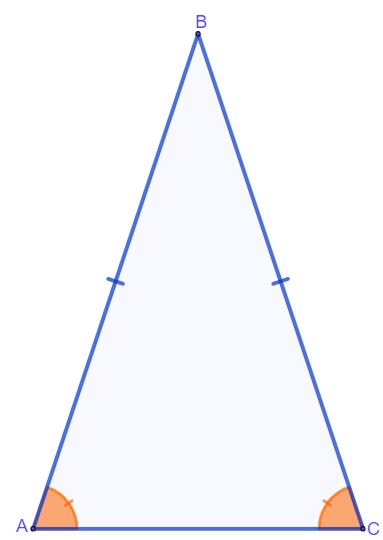
Vejamos, a seguir, uma aplicação dessa propriedade:
Exemplo: um triângulo isósceles possui o ângulo oposto à base medindo 70º, encontre o valor dos seus outros dois ângulos.
Resolução:
Como o triângulo é isósceles, então os ângulos da base medem x. Sabendo que a soma dos ângulos internos de um triângulo é sempre 180º, então, temos que:
x + x + 70º = 180º
2x = 180º – 70º
2x = 110
x = 110 : 2
x = 55°
Dessa forma, os ângulos da base medem 55° cada.
2ª propriedade: quando o triângulo é isósceles, a altura relativa à base do triângulo é também a mediana e a bissetriz.
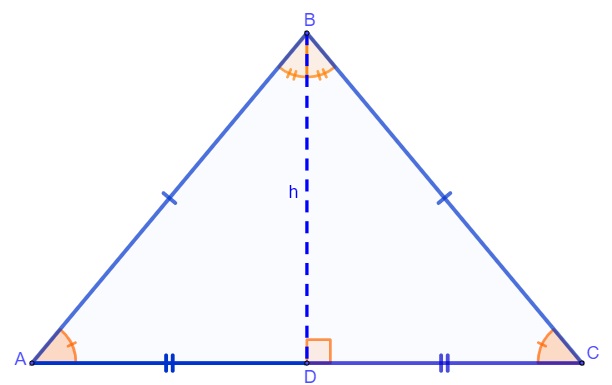
O segmento BD é a altura do triângulo, além disso, ele é bissetriz, pois divide o ângulo B em dois ângulos congruentes, e também é mediana, pois D é ponto médio do lado AC.
3ª propriedade: a altura divide o triângulo em dois triângulos congruentes.
Analisando a imagem anterior, é possível perceber que os triângulos ADB e CDB são congruentes pelo caso lado, lado e lado, logo, ao traçar a altura, dividimos o triângulo em dois triângulos retângulos congruentes.
Leia mais: Como identificar a mediana, a bissetriz e a altura de um triângulo
Fórmulas do triângulo isósceles
A seguir, veremos as fórmulas para o cálculo de área e perímetro do triângulo isósceles.
-
Perímetro do triângulo isósceles
O perímetro de um triângulo isósceles, assim como em qualquer polígono, é a soma dos seus lados. Como dois lados do triângulo são congruentes, temos que:
|
P = 2l + b |
Exemplo: um triângulo isósceles possui lados oblíquos medindo 15 cm e base medindo 10 cm, então, qual é o seu perímetro?
Resolução:
P = 2l + b
P = 2 · 15 + 10
P = 30 + 10
P = 40 cm
-
Área do triângulo isósceles
O cálculo da área do triângulo isósceles não se difere em relação à área dos outros triângulos, então, ela é calculada pelo produto entre a base e a altura dividido por 2.
![]()
Exemplo: calcule a área do triângulo isósceles que possui altura igual a 15 cm e base igual a 8 cm.
Resolução:
Calculando a área, temos que b = 8 e h = 15.
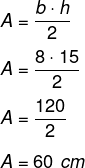
Classificação dos triângulos
Quando analisamos os lados dos triângulos, existem três classificações possíveis:
-
Equilátero: quando todos os seus lados são congruentes.
-
Escaleno: quanto todos os seus lados possuem medidas distintas.
-
Isósceles: quando há dois lados congruentes.
Outra classificação possível para o triângulo é quando analisamos seus ângulos. Assim, um triângulo pode ser:
-
Acutângulo: quanto todos os seus ângulos internos são agudos.
-
Retângulo: quando um dos seus ângulos internos é reto.
-
Obtusângulo: quando um dos seus ângulos internos é obtuso.
Caso queira saber mais sobre o tema deste tópico, leia: Classificação dos triângulos.
Exercícios resolvidos sobre triângulo isósceles
Questão 1
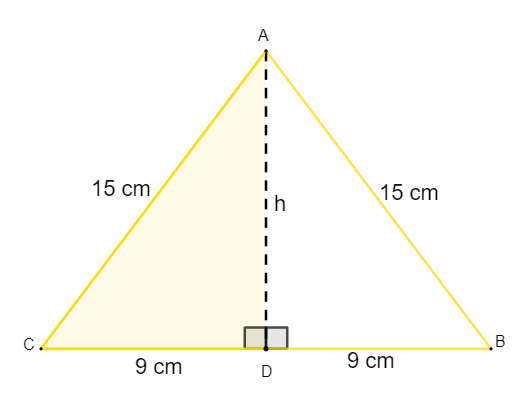
Dado o triângulo isósceles a seguir, a sua área é igual a:
A) 216 cm²
B) 182 cm²
C) 135 cm²
D) 108 cm²
E) 96 cm²
Resolução:
Alternativa D
Para calcular a área, é necessário, antes, descobrir a medida da altura h do triângulo. Para isso, aplicaremos o teorema de Pitágoras no triângulo ACD.
15² = 9² + h²
225 = 81 + x²
225 – 81 = h²
144 = h²
h² = 144
h = √144
h = 12
Conhecendo a altura, 12 cm, e sabendo que a base mede 18 cm, é possível calcular a área:
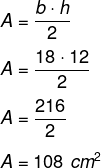
Questão 2
Um triângulo isósceles possui o ângulo do vértice que mede o triplo do ângulo da base, então, a medida do ângulo da base é:
A) 36°
B) 42°
C) 45°
D) 50°
E) 62°
Resolução:
Alternativa A
Sabemos que a soma dos ângulos internos é 180°.
Seja x a medida do ângulo da base, temos que:
x + x + 3x = 180°
5x = 180º
x = 180 : 5
x = 36°
Por Raul Rodrigues de Oliveira
Professor de Matemática
Fonte: Brasil Escola - https://brasilescola.uol.com.br/matematica/o-triangulo-isosceles-suas-particularidades.htm