Polígonos

Polígonos são figuras planas fechadas por segmentos de reta, com lados e vértices, e recebem nomes conforme a quantidade de lados, como o triângulo, que tem três lados; a quadrilátero, que tem quatro lados; o pentágono, com cinco lados, entre outros. Eles podem ser classificados em convexos ou não convexos, regulares ou irregulares. Seus principais elementos são lados, vértices, ângulos internos e externos, e diagonais.

Leia também: O que são as formas geométricas?

Resumo sobre polígonos

• Os polígonos são figuras planas fechadas por segmentos de reta.
• Os polígonos são nomeados de acordo com o número de lados.
• Os polígonos podem ser classificados como convexos e não convexos e como regulares e irregulares.
• Os principais elementos dos polígonos são vértices, lados, ângulos internos e externos, e diagonais.
• A soma dos ângulos internos de um polígono de n lados é calculada por (n - 2) ⋅ 180.
• A soma dos ângulos externos de um polígono é igual a 360º.
• A área e o perímetro do polígono dependem diretamente da forma geométrica.
• O número de diagonais do polígono é calculado por \(\frac {n(n-3)}2\).
• Além dos polígonos, existem os poliedros, sólidos geométricos tridimensionais.

O que são polígonos?

Os polígonos são figuras geométricas planas, fechadas e formadas apenas por segmentos de reta que se encontram nas extremidades — encontro conhecido como vértice. Esses segmentos são chamados de lados do polígono.

Para uma figura ser considerada um polígono, precisa ser plana, fechada e formada somente por segmentos de reta. O quadrado, o triângulo, o retângulo, o losango, entre outros exemplos, são polígonos presentes no nosso cotidiano. A circunferência, por exemplo, não é um polígono, pois não é formada por segmentos de reta.

Nomes dos polígonos

3 lados – triângulo

4 lados – quadrilátero

5 lados – pentágono

6 lados – hexágono

7 lados – heptágono

8 lados – octógono

9 lados – eneágono

10 lados – decágono

11 lados – undecágono

12 lados – dodecágono

13 lados – tridecágono

14 lados – tetradecágono

15 lados – pentadecágono

16 lados – hexadecágono

17 lados – heptadecágono

18 lados – octadecágono

19 lados – eneadecágono

20 lados – icoságono

Nomenclatura dos polígonos

A nomenclatura dos polígonos segue uma convenção antiga, baseada em prefixos para indicar o número de lados e no sufixo gono, que significa ângulo. Portanto, polígono pode ser entendido como figura de vários ângulos. Os únicos polígonos que fogem dessa regra são o triângulo e os quadriláteros, já os demais têm como regra a nomenclatura formada por:

PREFIXO COM NÚMERO DE LADOS + SUFIXO GONO

Número de lados	Prefixo	Nome
5	Penta	Pentágono
6	Hexa	Hexágono
7	Hepta	Heptágono
8	Octa	Octógono
9	Enea	Eneágono
10	Deca	Decágono

Elementos de um polígono

Os principais elementos dos polígonos são vértices, lados, ângulos internos e externos, e diagonais. Vamos aprender sobre cada um deles a seguir, e, para isso, vamos analisar este polígono:

• Lados: são os segmentos de reta \(\overline{AB},\ \overline{BC},\ \overline{CD},\ \overline{DE},\ \overline{EA} \).
• Vértices: são os pontos A, B, C, D, E.
• Diagonal: é o segmento de reta que liga dos vértices não colineares.

Vamos traçar as diagonais deste polígono:

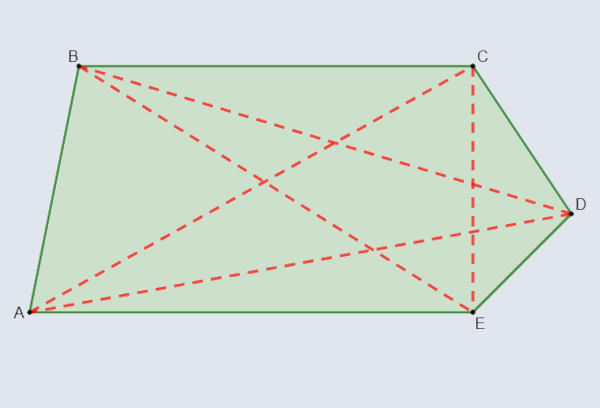
• Ângulos internos: são os ângulos formados pela interseção de dois lados consecutivos do polígono:

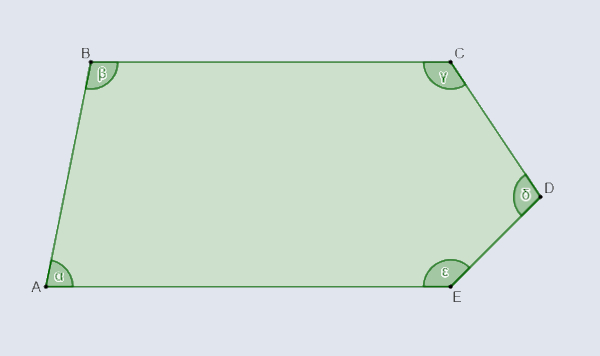
Classificação dos polígonos

Os polígonos são classificados de acordo com o número de lados e podem ser:

Tipos de polígonos

Existem duas maneiras importantes de se classificar os polígonos. O polígono pode ser regular ou irregular, e pode ser convexo ou não convexo (côncavo).

→ Polígono regular e polígono irregular

Essa classificação leva em consideração a medida dos lados do polígono. O polígono é conhecido como regular quando ele tem todos os lados e ângulos internos congruentes, ou seja, com a mesma medida; caso contrário, o polígono é conhecido como irregular.

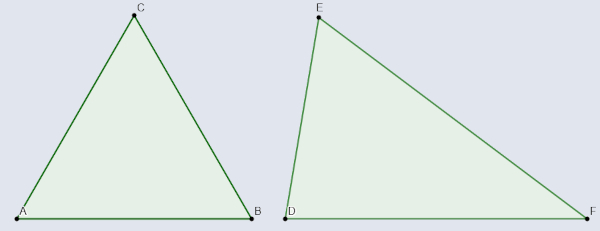
→ Polígono convexo e polígono não convexo

Essa classificação leva em consideração a medida dos ângulos do polígono. O polígono é convexo se todos os seus ângulos internos forem menores que 180º. Além disso, se você ligar dois pontos quaisquer dentro do polígono, o segmento estará sempre completamente dentro da figura; caso contrário, o polígono é não convexo ou côncavo.

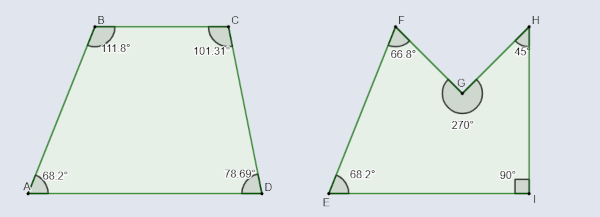
Acesse também: Tipos de polígonos — mais detalhes sobre os seus tipos

Soma dos ângulos internos de um polígono

Para calcular o valor da soma dos ângulos internos de um polígono, basta utilizar o número de lados na fórmula a seguir:

S_i = (n - 2) ⋅ 180

• Si → soma dos ângulos internos do polígono
• n → número de lados do polígono

Exemplo 1:

Qual é o valor da soma dos ângulos internos de um pentágono?

Resolução:

Sabemos que o pentágono tem cinco lados, logo, temos que:

n = 5

S_i = n - 2 ⋅ 180

S_i = (5 - 2) ⋅ 180

S_i = 3 ⋅ 180

S_i = 540

Então a soma dos ângulos internos de um pentágono é sempre igual a 540º.

• Exemplo 2:

Qual é o valor da soma dos ângulos internos de um triângulo?

Resolução:

Sabemos que o triângulo tem três lados, então temos que:

n = 3

S_i = (n - 2) ⋅ 180

S_i = (3 - 2) ⋅ 180

S_i = 1 ⋅ 180

S_i = 180

Então a soma dos ângulos internos de um triângulo é 180º.

Soma dos ângulos externos de um polígono

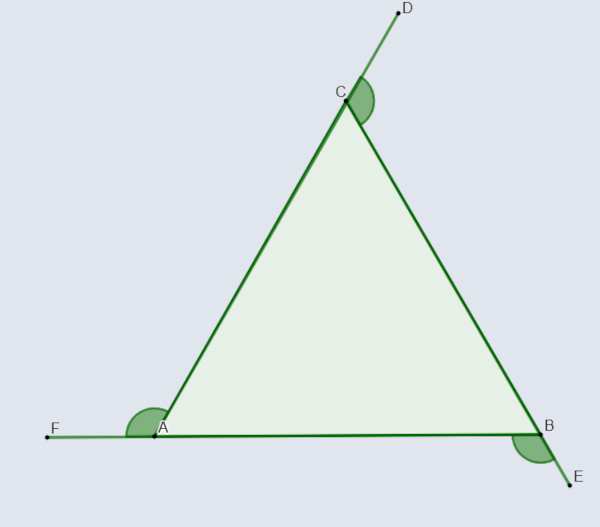
Os ângulos externos de um polígono são os ângulos formados entre um lado do polígono e a extensão do lado adjacente em qualquer polígono. A soma dos ângulos externos é sempre igual a 360°.

Diagonais dos polígonos

A diagonal é o segmento de reta que liga dois vértices não consecutivos do polígono. O número de diagonais de um polígono pode ser calculado pela fórmula:

\(d = \frac{n \cdot (n - 3)}{2}\)

• d → número de diagonais do polígono.
• n → número de lados do polígono.

• Exemplo 1:

Quantas diagonais tem um hexágono?

Resolução:

Sabendo que o hexágono tem seis lados, então temos que:

n = 6

\(d = \frac{6 \cdot (6 - 3)}{2}\)

\(d = \frac{6 \cdot 3}{2}\)

\(d = \frac{18}{2} \)

\(d=9 \)

Então o hexágono tem nove diagonais.

• Exemplo 2:

Quantas diagonais tem um pentágono?

Resolução:

Temos n = 5, logo:

\(d = \frac{5 \cdot (5 - 3)}{2}\)

\(d = \frac{5 \cdot 2}{2} \)

\(d=5 \)

Então o pentágono tem cinco diagonais.

Perímetro dos polígonos

Uma grandeza importante, o perímetro do polígono é igual à soma dos seus lados. O perímetro é mensurado em unidades de comprimento, como o milímetro, centímetro, metro, quilômetro. Para calcular o perímetro de determinado polígono, basta realizar a soma da medida dos lados.

• Exemplo:

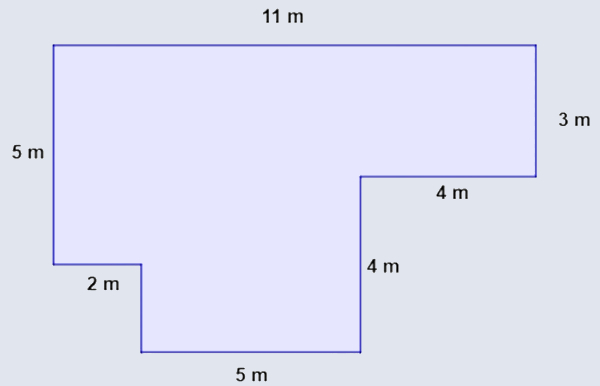
Calculando o perímetro desse polígono, temos que:

P = 5 + 11 + 3 + 4 + 4 + 5 + 2

P = 16 + 3 + 4 + 4 + 5 + 2

P = 19 + 4 + 4 + 5 + 2

P = 23 + 4 + 5 + 2

P = 27 + 5 + 2

P = 32 + 2

P = 34 m

Área dos polígonos

Cada polígono tem uma fórmula específica para o cálculo da sua área. Confira algumas a seguir.

→ Área do triângulo

O cálculo da área de um triângulo é feito multiplicando a base pela altura, dividido por 2, ou seja:

\(A = \frac{b \ \cdot \ h}{2} \)

• Exemplo:

Calcule a área do triângulo a seguir:

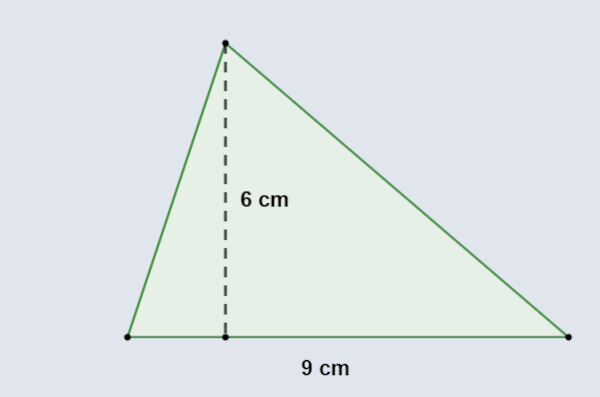
Resolução:

Sabemos que a altura mede 6 cm e a base mede 9 cm, então temos que:

\(A = \frac{9 \ \cdot \ 6}{2} \)

\(A = \frac{54}{2}\)

\(A = 27 \, \text{cm}^2 \)

→ Área do retângulo

A área do retângulo é calculada pelo produto entre a base e a altura do retângulo, ou seja:

A = b ⋅ a

• Exemplo:

Calcule a área do retângulo a seguir:

Resolução:

Como a base mede 9 e a altura mede 6, então temos que:

A= 9 ⋅ 6

A = 54 cm²

→ Área do quadrado

A área do quadrado é calculada elevando a medida do lado ao quadrado. Então temos que:

A = l²

• Exemplo:

Calcule a área do quadrado a seguir:

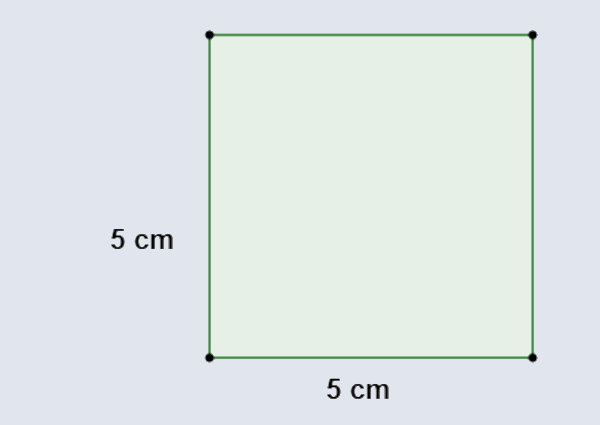
Resolução:

O lado desse quadrado mede 5 cm, então temos que:

A = l²

A = 5²

A = 25 cm²

→ Área do trapézio

A área do trapézio é calculada pela fórmula:

\(A = \frac{(B + b) \cdot h}{2}\)

• Exemplo:

Qual é a área do trapézio a seguir?

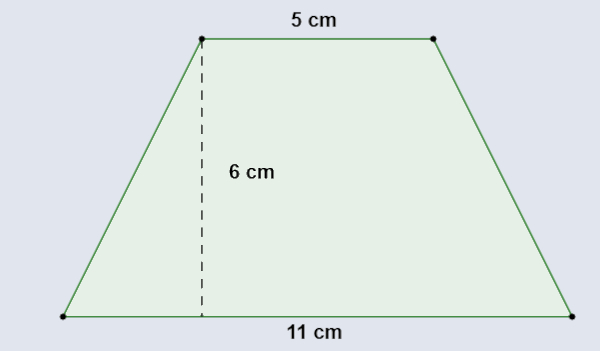
Resolução:

Temos que:

B = 11

h = 6

b = 5

Substituindo na fórmula:

\(A = \frac{(11 + 5) \cdot 6}{2}\)

\(A = \frac{16 \cdot 6}{2}\)

\(A=16 \cdot 3\)

\(A=48 cm^2\)

→ Área do losango

A área do losango é igual ao produto entre a diagonal maior D e a diagonal d, dividido por 2, então temos que:

\(A = \frac{D \cdot d}{2}\)

• Exemplo:

Qual é a área do losango a seguir?

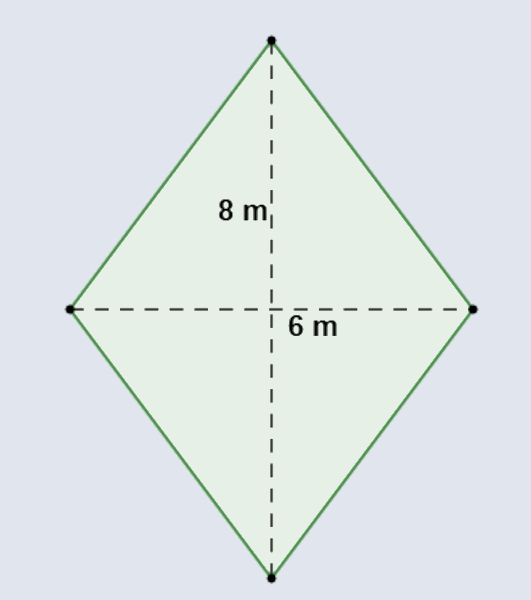
Resolução:

Sabemos que:

D = 8

d = 6

Então:

\(A = \frac{8 \ \cdot \ 6}{2}\)

\(A = \frac{8 \ \cdot \ 6}{2}\)

\(A = 24 \, \text{m}^2\)

Diferenças entre polígonos e poliedros

Os polígonos são figuras geométricas planas, têm somente duas dimensões, como os quadriláteros, os triângulos, os pentágonos, entre outros. Já os poliedros são sólidos geométricos espaciais, têm três dimensões, como o cubo, a pirâmide e os prismas.

Observe o exemplo a seguir:

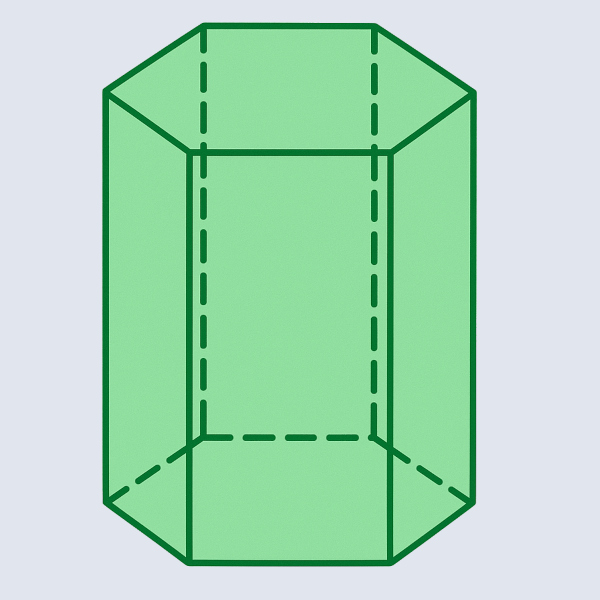
Note que todas as faces de um poliedro são formadas por um polígono. Nesse exemplo ele é formado por hexágonos e retângulos.        

Acesse também: Poliedros — mais detalhes sobre essas figuras tridimensionais

Exercícios resolvidos sobre polígonos

Questão 1

Um polígono tem soma dos ângulos internos igual a 1800º, então o número de lados desse polígono é:

A) 8

B) 10

C) 12

D) 15

E) 20

Resolução:

Alternativa C.

Sabemos que:

\(S_i = (n - 2) \cdot 180\)

Nesse caso, temos que:

\(S_1=1800\)

Então temos que:

\(1800 = (n - 2) \cdot 180\)

\(\frac{1800}{180} = n - 2\)

\(10=n-2\)

\(10+2=n\)

\(12=n\)

\(n=12\)

Então esse polígono tem 12 lados.

Questão 2

O polígono que tem o número de diagonais igual ao número de lados é o:

A) Triângulo

B) Quadrilátero

C) Pentágono

D) Hexágono

E) Eneágono

Resolução:

Alternativa C.

Sabemos então que d = n, substituindo na fórmula temos que:

\(d = \frac{n \ \cdot \ (n - 3)}{2}\)

\(n = \frac{n \ \cdot \ (n - 3)}{2} \)

\(2n=n \cdot (n-3)\)

\(\frac{2n}{n} = n - 3\)

\(2=n -3\)

\(2 +3=n\)

\(5=n\)

\(n=5\)

O polígono que tem cinco lados é o pentágono.

Fontes

DANTE, Luiz Roberto. Matemática: Contexto e Aplicações. 3. ed. São Paulo: Ática, 2016.

IEZZI, Gelson; MURAKAMI, Carlos. Fundamentos da Matemática Elementar: Geometria Plana. 8. ed. São Paulo: Atual, 2005.