Ciclo de Carnot

O ciclo de Carnot é um ciclo termodinâmico que idealiza o máximo que uma máquina térmica consegue converter de calor em trabalho. Ele possui quatro fases:

• expansão isotérmica reversível;
• expansão adiabática reversível;
• compressão isotérmica reversível;
• compressão adiabática reversível.

Leia também: Termodinâmica — área da Física que estuda as trocas de calor e energia

Resumo sobre o ciclo de Carnot

• O ciclo de Carnot funciona por meio do revezamento de compressões e expansões isotérmicas e adiabáticas.
• O processo isotérmico é aquele em que a temperatura é constante.
• O processo adiabático é o que não permite trocas de calor com o ambiente.
• O ciclo de Carnot foi formulado por Nicolas Sadi Carnot.
• A teoria de Carnot foi desenvolvida visando a encontrar o valor máximo do rendimento dos motores térmicos, que funcionam entre uma fonte quente e uma fonte fria.
• O ciclo de Carnot é reversível, já que pode ser invertido.
• As máquinas de Carnot apresentam maior rendimento do que as máquinas térmicas irreversíveis.
• Elas são as máquinas térmicas que operam por meio do ciclo de Carnot e são capazes de converter o máximo de calor em trabalho.
• O rendimento de uma máquina de Carnot pode ser calculado em termos de temperatura ou calor da fonte fria e da fonte quente.

Quais são as etapas do ciclo de Carnot?

O ciclo de Carnot é um ciclo reversível que funciona por meio de duas transformações gasosas que se alternam em quatro etapas, independentemente da substância empregada, conforme podemos observar na imagem abaixo:

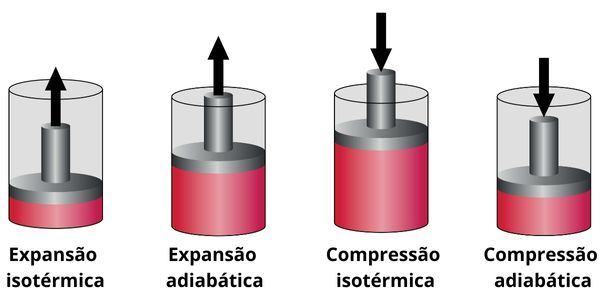
• 1ª etapa, do ponto 1 → 2 : acontece uma expansão isotérmica (processo em que a temperatura é constante) reversível, caracterizada pelo gás (ou sistema) realizar trabalho e ganhar uma quantidade de calor da fonte quente.
• 2ª etapa, do ponto 2 → 3 : acontece uma expansão adiabática (processo em que não há trocas de calor com o meio externo) reversível, caracterizada por não ocorrer troca de calor com as fontes térmicas. Contudo, ocorre realização de trabalho pelo gás, diminuindo a sua energia interna e gerando decréscimo em sua temperatura.
• 3ª etapa, do ponto 3 → 4 : acontece uma compressão isotérmica reversível, caracterizada pelo gás adquirir trabalho e doar uma quantidade de calor à fonte fria.
• 4ª etapa, do ponto 4 → 1 : acontece uma compressão adibática reversível, caracterizada por não ocorrer troca de calor com as fontes térmicas. Contudo, temos o aquecimendo do gás até que atinja a mesma temperatura da fonte quente e, assim, ser posto em contato com ela, concluindo o ciclo.

Assim, é possível descrever o ciclo de Carnot por meio de um gráfico da pressão pelo volume (p x V ), como podemos ver abaixo:

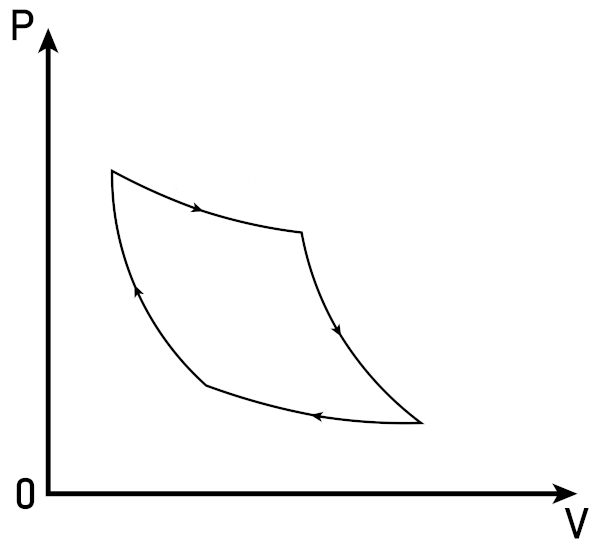
O que diz a teoria de Carnot?

A teoria de Carnot foi formulada, em 1824, pelo cientista Nicolas Sadi Carnot (1796-1832), que procurava obter o rendimento máximo que uma máquina térmica consegue operar. Para tanto, ele percebeu que seria necessário que o processo ocorresse de maneira reversível, podendo ser invertido.

Com base nisso, ele formulou o ciclo de Carnot, que se divide em dois postulados, os quais descrevem a operação das máquinas térmicas de Carnot e a sua superioridade em relação às máquinas térmicas irreversíveis:

“Nenhuma máquina térmica que opere entre uma dada fonte quente e uma dada fonte fria pode ter rendimento superior ao de uma máquina de Carnot.”

 “Todas as máquinas de Carnot que operem entre essas duas fontes terão o mesmo rendimento.”|1

Ainda que não tenha compreendido a primeira lei da termodinâmica, Carnot foi capaz de formular as bases da segunda lei da termodinâmica, sendo considerado o seu fundador.

Leia também: Trabalho mecânico — grandeza que permite calcular a variação de energia sofrida por um corpo

Máquina de Carnot

A máquina de Carnot é uma máquina térmica teórica que funciona com base no ciclo de Carnot, em que ela recebe calor de um reservatório quente, transformando-o em trabalho, e o que sobra ela transfere para um reservatório frio.

Ela é capaz de atingir o ápice do rendimento na conversão de calor em trabalho, não atingindo 100%, já que, para isso, ela teria que constestar a segunda lei da termodinâmica, que dita as condições necessárias para a transformação do calor em trabalho, e a terceira lei da termodinâmica, alcançando o zero absoluto.

• Qual a fórmula do rendimento da máquina de Carnot?

A fórmula do rendimento de uma máquina de Carnot foi desenvolvida com base na ideia de que a quantidade de calor da fonte fria dividida pela quantidade de calor da fonte quente é proporcional à temperatura da fonte fria dividida pela temperatura da fonte quente:

 \(\frac{\left|Q_F\right|}{\left|Q_Q\right|}=\frac{T_F}{T_Q}\)

• \(\left|Q_F\right|\) é o módulo do calor da fonte fria, medido em Joules [J] .
• \(\left|Q_Q\right| \)  é o módulo do calor da fonte quente, medido em Joules [J] .
• T_F  é a temperatura da fonte fria, medida em Kelvin [K] .
• T_Q  é a temperatura da fonte quente, medida em Kelvin [K] .

Então, o rendimento de uma máquina de Carnot pode ser dado em termos das temperaturas da fonte fria e da fonte quente:

 \(\eta=1-\frac{T_F}{T_Q}\)

• η  é o rendimento da máquina térmica.
• T_F  é a temperatura da fonte fria, medida em Kelvin [K] .
• T_Q  é a temperatura da fonte quente, medida em Kelvin [K] .

O rendimento de uma máquina de Carnot também pode ser dado em termos do calor da fonte fria e da fonte quente:

\(\eta=1-\frac{\left|Q_F\right|}{\left|Q_Q\right|}\)

• η  é o rendimento da máquina térmica.
• \(\left|Q_F\right|\)  é o módulo do calor da fonte fria, medido em Joules [J] .
• \(\left|Q_Q\right| \)  é o módulo do calor da fonte quente, medido em Joules [J] .

Além disso, também podemos calcular o rendimento por meio de:

\(\eta=\frac{W}{Q_Q}\)

• η  é o rendimento da máquina térmica.
• W  é o trabalho do gás, medido em Joules J.
• Q_Q é o calor da fonte quente, medido em Joules [J] .

O trabalho no ciclo de Carnot é dado pela área do gráfico:

W≅ área do gráfico

• W  é o trabalho do gás, medido em Joules J.

Exercícios resolvidos sobre o ciclo de Carnot

Questão 1

Qual a temperatura da fonte quente de uma máquina de Carnot, sabendo que a temperatura da fonte fria é de 300 K  e seu rendimento é de 75 % ?

a) 2250 K

b) 450 K

c) 1200 K

d) 380 K

e) 3640 K

Resolução:

Alternativa C. Calcularemos a temperatura da fonte quente por meio da fórmula de rendimento de uma máquina de Carnot:

\(\eta=1-\frac{T_F}{T_Q}\)

 75%= \(1-\frac{300}{T_Q}\)

\(\frac{75}{100}=1-\frac{300}{T_Q}\)

\(0,75=1-\frac{300}{T_Q}\)

\(0,75-1=-\frac{300}{T_Q}\)

\(-0,25=-\frac{300}{T_Q}\)

\(0,25=\frac{300}{T_Q}\)

\(T_Q=\frac{300}{0,25}\)

\(T_Q=1200\ K\)

Questão 2

(UEMG) Uma máquina térmica que opera segundo o ciclo de Carnot executa 10 ciclos por segundo. Sabe-se que, em cada ciclo, ela retira 800 J da fonte quente e cede 400 J para a fonte fria. Se a temperatura da fonte fria é igual a 27 °C, o rendimento dessa máquina e a temperatura da fonte quente valem, respectivamente,

a) 20%; 327 K.

b) 30%; 327 K.

c) 40%; 700 K.

d) 50%; 600 K.

Resolução:

Alternativa D. Primeiramente converteremos a temperatura de Celsius para Kelvin:

\(27\ °C=300 K\)

Então calcularemos a temperatura da fonte quente utilizando a fórmula geral da máquina térmica:

\(\frac{\left|Q_F\right|}{\left|Q_Q\right|}=\frac{T_F}{T_Q}\)

\(\frac{\left|400\right|}{\left|800\right|}=\frac{300}{T_Q}\)

\(0,5=\frac{300}{T_Q}\)

\(T_Q=\frac{300}{0,5}\)

\(T_Q=600\ K\)

Depois calcularemos o rendimento dessa máquina:

\(\eta=1-\frac{T_F}{T_Q}\)

\(\eta=1-\frac{300}{600}\)

\(\eta=1-0,5\)

\(\eta=0,5\)

ou:

\(\eta=50%\)

Nota

|1| Ambas citações foram retiradas do livro Fundamentos da Física: Gravitação, Ondas e Termodinâmica (vol. 2).

Por Pâmella Raphaella Melo
Professora de Física