Margem de erro de uma pesquisa
A margem de erro é aplicada em pesquisas estatísticas para nos mostrar quais são as possíveis variações dos resultados obtidos.
A margem de erro de uma pesquisa é a estimativa estatística que determina o erro amostral da pesquisa e nos permite saber qual é o intervalo de confiança de seus dados. A maioria das pesquisas é realizada com uma amostra, já que não é possível consultar toda a população. Por meio da amostra aleatória é possível fazer inferências sobre o resultado esperado na população, e a margem de erro é a estatística que analisa os possíveis erros amostrais, tornando possível encontrarmos um intervalo de confiança.
Leia também: Como funciona o sistema eleitoral brasileiro?
O que é margem de erro?
Quando um instituto decide realizar uma pesquisa, por questões financeiras, geográficas, entre outras, muitas vezes não é possível consultar toda a população. Por exemplo, se a pesquisa quer verificar a intenção de votos em um candidato a governador, não é possível checar qual é a intenção de voto de todos os moradores do estado, surgindo então a necessidade de escolher uma amostra para essa pesquisa.
Ao escolhemos essa amostra, é necessário que a escolha seja totalmente aleatória, levando em consideração as diferentes características da população — por exemplo, entrevistar pessoas de diferentes classes, gêneros, raças, cidades; enfim, buscar uma amostra que seja significativa e represente aquela comunidade.
Após a coleta de dados, como a pesquisa foi feita com uma amostra, existem erros amostrais que podem ter sido cometidos, o que faz com que a amostra não represente 100% a população. Surge, então, a necessidade de estabelecer uma margem de erro.
A margem de erro nos diz qual é a possibilidade de variação dos resultados coletados. Por exemplo, as pesquisas eleitorais possuem quase sempre margem de erro de 2%, o que significa que os resultados encontrados para cada variável podem ser no máximo 2% maiores ou no mínimo 2% menores do que o apresentado pela pesquisa.
Assim, a margem de erro é uma estimativa estatística que nos permite analisar as pesquisas e refletir sobre a confiança dos resultados obtidos. Se uma pesquisa tem uma margem de erro muito grande, significa que a variação entre os dados pode ser extensa, o que diminui a precisão dessa pesquisa, pois quanto menor a margem de erro, mais precisos são os dados da pesquisa.
Margem de erro e intervalo de segurança
Conhecendo a margem de erro da pesquisa, é possível calcular o intervalo de segurança, conhecido também como intervalo de confiança da pesquisa. Para compreender o que é o intervalo de segurança, veremos um exemplo a seguir.
Exemplo: Suponha que em uma eleição para governador de Goiás, há 3 possíveis candidatos, o candidato A, o candidato B e o candidato C, e várias pesquisas foram realizadas contabilizando a intenção de voto dos eleitores ao decorrer dos dias, como mostra o gráfico a seguir:
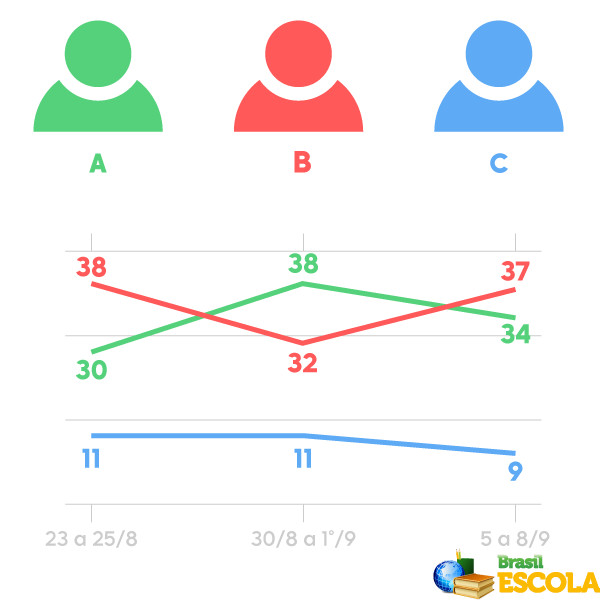
Se a margem de erro dessa pesquisa for de 2%, podemos encontrar o intervalo de segurança para a intenção de voto dos goianos para cada um dos candidatos.
Note que o candidato A possui na última semana uma intenção de voto de 34%, com a margem de erro de 2%. Isso significa que o intervalo de segurança é de 34%±2%, o que quer dizer que o resultado do candidato A pode chegar no máximo até 36% e no mínimo até 32%.
Fazendo a mesma análise para o candidato B, o intervalo de confiança é 37%±2%, chegando no máximo a 39% e no mínimo a 35%.
Podemos afirmar que os candidatos A e B estão empatados dentro da margem de erro. Isso significa que os intervalos de segurança do candidato A e do candidato B possuem valores em comum, tornando possível que eles alcancem a mesma porcentagem na pesquisa.
Analisando o candidato C, percebemos que ele possui uma intenção de voto de 9%±2%, podendo alcançar no máximo 11% e no mínimo 7%.
Leia também: Gráficos — ferramenta amplamente utilizada para analisar dados
Como ler a margem de erro de uma pesquisa?
A margem de erro, de forma geral, nos permite descobrir o intervalo de segurança, sendo possível prever entre quais valores está o resultado da pesquisa quando comparamos a amostra com a população. Seja m% a margem de erro e p% a porcentagem encontrada na pesquisa para uma determinada variável, o intervalo de confiança dessa variável é dado por:
\((p±m)%\)
Então, suponha que em uma pesquisa sobre a satisfação dos clientes de uma empresa a margem de erro seja de 4%. Logo, se 32% dos clientes se sentem satisfeitos, isso significa que podemos ter 36% dos clientes satisfeitos no máximo ou 26% dos clientes satisfeitos no mínimo.
Como calcular a margem de erro
O cálculo da margem de erro é feito por estatísticos, que utilizam conhecimentos aprendidos a nível superior para entender a distribuição dos dados coletados e calcular a margem de erro, que é dada pela fórmula:
\(z⋅\frac{σ}{\sqrt{n}}\)
-
n: é o tamanho da amostra.
-
σ: é o desvio padrão populacional.
-
z: é o score do nível de confiança desejado.
Para encontrar z é necessário consultar uma tabela de distribuição normal padrão, e o seu valor depende diretamente do nível de confiança desejado para os dados. Isso quer dizer que se a pesquisa tem 95% de confiança, usaremos um valor pra z, que é 1,96 (encontrado ao consultarmos a tabela de distribuição normal padrão). Para valores diferentes de nível de confiança da pesquisa, temos valores diferentes para z. Normalmente, para calcular a margem de erro, os institutos de pesquisa utilizam programas que já oferecem o cálculo da margem de erro, de acordo com o valor da amostra, do desvio padrão e do nível de confiança desejado.
Importância da margem de erro de uma pesquisa
Analisando a margem de erro, é possível avaliar qual é o grau de confiança e precisão que os resultados encontrados na pesquisa passam. Se a margem de erro for muito alta, teremos um intervalo de confiança muito grande, o que é ruim, pois os dados encontrados na pesquisa serão poucos precisos.
Uma pesquisa sem margem de erro pode não condizer com a realidade, porque não é possível saber qual é o intervalo de confiança dos dados encontrados e nem mesmo se esses dados são satisfatoriamente precisos. Assim, a margem de erro de uma pesquisa é importante para analisarmos a precisão dos dados e verificarmos o intervalo de confiança.
Por Raul Rodrigues de Oliveira
Professor de Matemática
Fonte: Brasil Escola - https://brasilescola.uol.com.br/matematica/o-que-margem-erro-uma-pesquisa.htm