Aplicações da força centrípeta em lombadas e depressões

A aplicação da força centrípeta em lombadas e depressões ocorre da seguinte forma: nas lombadas, a força centrípeta é igual à diferença entre a força peso e a força normal. Nas depressões, a força centrípeta é igual à diferença entre a força normal e a força peso. A força centrípeta é uma grandeza física responsável por alterar o sentido e direção do vetor velocidade do corpo, direcionando-o para o centro da trajetória circular. Em razão disso, ela possui diversas aplicações, como é o caso das lombadas e depressões.

Leia também: O que é a força centrífuga?

Resumo sobre aplicações da força centrípeta em lombadas e depressões

• A força centrípeta é uma força que sempre aponta para o centro da trajetória.

• As lombadas são trechos elevados de concreto ou asfalto nas pistas.

• As depressões são trechos de declives nas pistas.

• Nas lombadas, a força peso é maior que a força normal.

• Nas depressões, a força normal é maior que a força peso.

O que é a força centrípeta?

A força centrípeta é uma força capaz de direcionar os corpos para o centro da trajetória durante uma rotação ou movimento circular. Ela é calculada por meio do produto da massa do corpo com a sua aceleração centrípeta, descrito pela fórmula abaixo:

\(F_{\text{CP}} = m \cdot a_{\text{CP}} \)

• \(F_{\text{CP}} \) é a força centrípeta, medida em Newton [N];

• m é a massa do corpo, medida em quilograma [kg];

• \(a_{\text{CP}} \) é a aceleração centrípeta, medida em \(m / {s} ^ {2}\).

A aceleração centrípeta pode ser calculada por meio da fórmula:

\(a_{\text{CP}} = \frac{m \cdot v^2}{R} \)

• m é a massa do corpo, medida em quilograma [kg];

• \(a_{\text{CP}} \) é a aceleração centrípeta, medida em \(m / {s} ^ {2}\);

• v é a velocidade escalar do corpo, medida em \(m / {s}.\)

• R é o raio da trajetória, medido em metros [m].

Ou da fórmula:

\(a_{\text{CP}} = \omega^2 \cdot R \)

• \(a_{\text{CP}} \) é a aceleração centrípeta, medida em \(m / {s} ^ {2}\);

• R é o raio da curva, medido em metros [m];

• ω é a velocidade angular, medida em \(rad /s \)

Como é a aplicação da força centrípeta em lombadas?

As lombadas, ou quebra-molas, são superfícies elevadas de concreto ou asfalto empregadas para diminuir a velocidade dos automóveis em ruas, avenidas e rodovias. Quando os automóveis passam por cima das lombadas, eles sofrem a ação de três forças: força peso, força normal e força centrípeta (nessa situação estamos desconsiderando as forças de atrito e resistência do ar), conforme descrito na imagem abaixo:

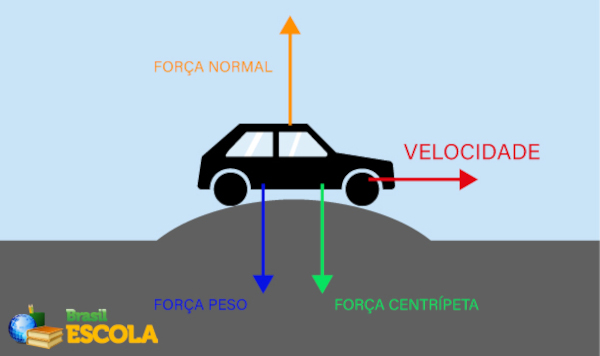
Nessa situação, a força peso exercida no automóvel é maior que a força normal exercida pela superfície no automóvel para mantê-lo na trajetória. E a força centrípeta aponta para baixo, já que ela sempre aponta para o centro da trajetória. Analisando essa situação é possível encontrarmos a fórmula que relaciona a força peso e a força normal à força centrípeta.

\(F_{R} = F_{CP} \)

\(P - N = m \cdot a_{\text{CP}} \)

• \({F_R}\) é a força resultante, medida em Newton [N];

• \(F_{CP} \) é a força centrípeta, medida em Newton [N];

• P é a força peso, medida em Newton [N];

• N é a força normal, medida em Newton [N];

• m é a massa do corpo, medida em quilograma [kg];

• \(a_{\text{CP}} \) é a aceleração centrípeta, medida em \(m / {s} ^ {2}\).

Exemplo: Determine a intensidade da força normal que a pista exerce sobre um carro de 1.000 kg que atravessa uma lombada de raio 100 m com velocidade de 30 m/s. Considere a aceleração da gravidade igual a \(10 {m} / {{s} ^ {2}}\).

\(F_{R} = F_{CP} \)

\(P - N = m \cdot a_{\text{CP}} \)

\(m \cdot g - N = \frac{m \cdot v^2}{R} \)

\(1000 \cdot 10 - N = \frac{1000 \cdot 30^2}{100} \)

\(10000-N=9000\)

\(N=10000-9000\)

\(N=1000 N\)

Saiba mais: Afinal, o que é força?

Como é a aplicação da força centrípeta em depressões?

As depressões são regiões esburacadas ou com declives existentes em diversas ruas, avenidas e rodovias. Quando os automóveis passam por cima das depressões, eles sofrem a ação de três forças: força peso, força normal e força centrípeta (nessa situação estamos desconsiderando as forças de atrito e resistência do ar), conforme descrito na imagem abaixo:

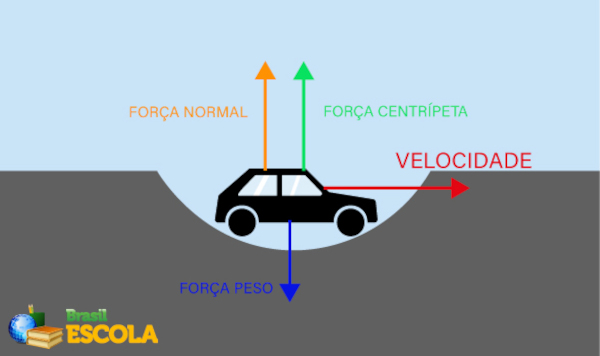
Nessa situação, a força normal exercida pela superfície no automóvel é maior que a força peso exercida no automóvel para mantê-lo na trajetória. E a força centrípeta aponta para cima, já que ela sempre aponta para o centro da trajetória. Analisando essa situação é possível encontrarmos a fórmula que relaciona a força peso e a força normal à força centrípeta.

\(F_{R} = F_{CP} \)

\(N - P = m \cdot a_{\text{CP}} \)

• \({F_R}\) é a força resultante, medida em Newton [N];

• \(F_{CP} \) é a força centrípeta, medida em Newton [N];

• N é a força normal, medida em Newton [N];

• P é a força peso, medida em Newton [N];

• m é a massa do corpo, medida em quilograma [kg];

• \(a_{\text{CP}} \) é a aceleração centrípeta, medida em \(m / {s} ^ {2} \).

Exemplo: Determine a intensidade da força normal que a pista exerce sobre um carro de 800 kg que atravessa um declive de raio 40 m com velocidade de 50 m/s. Considere a aceleração da gravidade igual a \(10 {m} / {{s} ^ {2}}\).

\(F_{R} = F_{CP} \)

\(N - P = m \cdot a_{\text{CP}} \)

\(N - m \cdot g = \frac{m \cdot v^2}{R} \)

\(N - 800 \cdot 10 = \frac{800 \cdot 50^2}{40} \)

\(N-8000=50000\)

\(N=50000+8000\)

\(N=58000 N\)

Aplicações da força centrípeta em outras situações do cotidiano

Existem diversas outras aplicações da força centrípeta no cotidiano. Pensando nisso, selecionamos algumas delas abaixo:

• globo da morte;

• curvas em estradas;

• brinquedo do parque de diversões chapéu mexicano;

• girar rapidamente um balde com água;

• esporte olímpico arremesso de peso.

Fontes

HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos da Física: Mecânica. 8. ed. Rio de Janeiro, RJ: LTC, 2009.

NUSSENZVEIG, H. M. Curso de física básica: Mecânica (vol. 1). 5 ed. São Paulo: Editora Blucher, 2015.