Área do cone

A área do cone é a medida da superfície desse sólido geométrico. Como o cone é formado por uma base circular e uma região lateral curva, sua área será a soma das áreas dessas duas regiões, chamadas, respectivamente, de área da base e área lateral.

Leia também: Como calcular o tronco de um cone

Resumo sobre a área do cone

• A medida da superfície do cone é a área desse corpo redondo.
• A superfície do cone é constituída por duas partes: a base e a lateral.
• Se r  é o raio da base do cone, então a área da base é dada por

\(A_b=πr^2\)

• Se g  é a geratriz do cone, então a área lateral é dada por

\(A_l=πrg\)

• A área total do cone é dada por

 \(A_t=πr^2+πrg=πr(r+g)\)

Videoaula sobre a área do cone

Planificação do cone

O cone é um corpo redondo formado por uma base circular e uma lateral curva (semelhante a um funil ou chapéu de aniversário). Assim, sua planificação é composta por duas partes: um círculo e setor circular.

A imagem abaixo apresenta o processo de planificação de um cone circular reto (no qual o segmento VO é perpendicular ao plano da base). À esquerda, temos um cone de altura h, raio da base r  e geratriz g. À direita temos a planificação desse cone. Perceba que a base formou um círculo de raio r,  e a lateral formou um setor circular de raio g e comprimento de arco 2πr  (que é o comprimento do círculo da base).

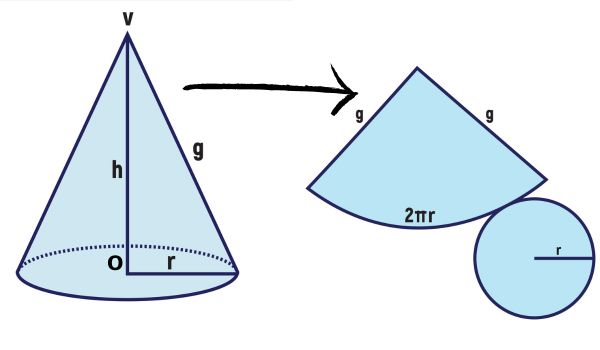
Qual a fórmula da área do cone?

Pela planificação do cone circular reto, concluímos que sua área é a soma da área da base e da área lateral.

A área da base de um cone é a área de um círculo de raio r . Portanto, a área da base Ab  de um cone é dada por

\(A_b=πr^2\)

Já a área lateral Al  é a área de um setor circular de raio g  e comprimento de arco 2πr . Como a área do setor é proporcional à área do círculo completo, podemos relacionar as respectivas áreas com os comprimentos dos arcos:

\( \frac{πg^2}{A_l } \frac{2πg}{2πr }\)

\(A_l=πrg\)

Logo, a fórmula da área do cone At  é dada por

\(A_t=A_b+A_l\)

\(A_t=πr^2+πrg\)

\(A_t=πr(r+g)\)

Como se calcula a área do cone?

Para calcular a área de um cone circular reto, basta substituir os dados do raio r  e da geratriz g .

Uma relação importante entre os segmentos do raio r, da altura h e da geratriz g nesse tipo de cone é que os três formam um triângulo retângulo. Assim, pelo Teorema de Pitágoras, temos que

\(g^2=h^2+r^2\)

Essa informação é muito útil caso a altura do cone seja conhecida mas a geratriz ou o raio não sejam conhecidos.

• Exemplo: Determine a área de um cone circular reto com 3 cm de raio da base e 4 cm de altura.

Para calcular a área desse cone precisamos da geratriz:

\(g^2=h^2+r^2\)

\(g^2=4^2+3^2\)

\(g=√25=5cm\)

Logo,

\(A_t=πr(r+g)\)

\(A_t=π⋅3(3+5)\)

\(A_t=24π cm²\)

Leia também: Como calcular o volume do cone

Exercícios resolvidos sobre a área do cone

Questão 1

(UFPI) Se 8π  cm² é a área lateral de um cone circular reto cujo raio da base é 2 cm, então a altura desse cone, em cm, é:

a) \( √2.\)

b) \( √3.\)

c) \( √6.\)

d) \( 2√2.\)

e) \( 2√3.\)

Resolução

Como a área lateral é 8π cm² e r = 2  cm, então g = 4  cm, pois

\(A_l=πrg\)

\(8π= π⋅2⋅g\)

\(g=4\)

Portanto,

\(g^2=h^2+r^2\)

\(4^2=h^2+2^2\)

\(h^2=12\)

\(h=2√3\)

Alternativa E.

Questão 2

(Unifor-CE – adaptado) Em um cone reto, a área da base é \(9π cm² \) e a geratriz mede \(3√10 cm\). A área desse cone, em centímetros quadrados, é

a) \( 9π(1+√10)\)

b) \( 3π(1+√10)\)

c) \( 3π(1+√3)\)

d) \( 9π(1+√3)\)

e) \( 10π(1+√3)\)

Resolução

Como a área da base é 9π  cm², então r=3  cm, pois

\(A_b=πr^2\)

\(9π=πr^2\)

\(r^2=9\)

\(r=3\)

Assim,

\(A_t=πr(r+g)\)

\(A_t=π⋅3(3+3√10)\)

\(A_t=9π+9π√10\)

\(A_t=9π(1+√10)\)

Alternativa A.

Fontes:

DANTE, L. R. Matemática: contexto & aplicações – Ensino Médio. 3. ed. São Paulo: Ática, 2016. v.3.

DOLCE, O; POMPEO, J. N. Fundamentos de matemática elementar, vol 10: Geometria espacial - Posição e métrica. 7 ed. Santos: Atual, 2013.