Força de atrito

A força de atrito é uma força de contato que resiste ao movimento dos corpos. Ela pode ser classificada como cinética ou estática. É influenciada pela força normal e pelo material dos corpos que estão atritando. Graças à sua existência, é possível que os automóveis, pessoas e objetos possam se mover.

Leia também: Leis de Newton — os postulados em torno da dinâmica do movimento dos corpos

Resumo sobre força de atrito

• A força de atrito é proporcional à força normal e ao coeficiente de atrito.

• É calculada pela multiplicação entre o coeficiente de atrito e a força normal.

• Pode ser cinética ou estática.

• A força de atrito cinética aparece sobre corpos em movimento.

• A força de atrito estática aparece sobre corpos que estão parados ou quase em movimento.

Videoaula sobre força de atrito

O que é força de atrito?

A força de atrito é uma força de contato entre corpos que se atritam. Ainda que tenhamos uma superfície aparentemente lisa, na verdade ela é composta por rugosidades que causam atrito, como podemos ver na imagem:

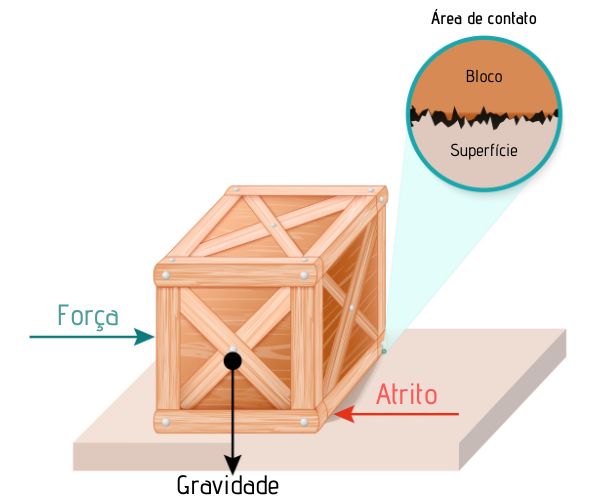
A orientação da força de atrito é:

• Sentido: contrário ao movimento, podendo ser para a direita ou para a esquerda, para frente ou para trás. Portanto, se a força é para frente, a força de atrito é para trás.

• Direção: a mesma do movimento, podendo ser horizontal ou vertical. Portanto, se o movimento é na horizontal, a força de atrito é na horizontal.

• Intensidade: encontrada por meio da fórmula da força de atrito.

Fatores que influenciam a força de atrito

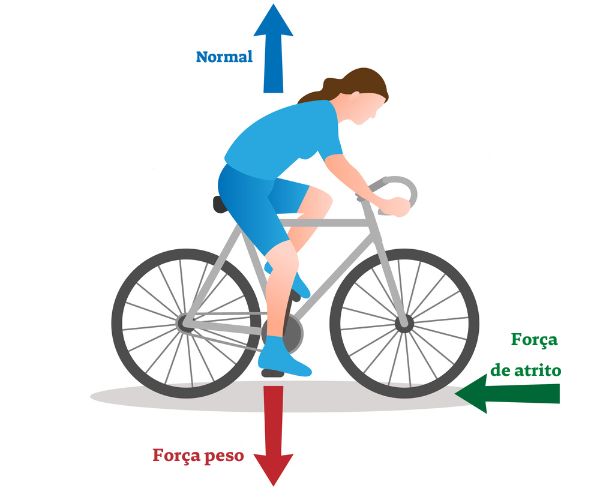
Existem dois fatores que influenciam a força de atrito: a força normal e o coeficiente de atrito.

• Força normal: é a força que a superfície faz sobre os corpos, mantendo-os suspensos. Ela é proporcional à força de atrito, sendo que ao aumentarmos a força normal, a força de atrito também aumenta.  

• Coeficiente de atrito: é uma propriedade das superfícies que representa a capacidade de oposição ao movimento, variando de acordo com o material dos corpos que estão atritando. Materiais mais polidos, como gelo e aço, possuem um coeficiente de atrito menor, gerando uma força de atrito menor, portanto o movimento ocorre com menos esforço.

Tipos de força de atrito

A força de atrito pode ser classificada de duas maneiras: estática ou cinética. A força de atrito estática atua sobre o corpo que está em repouso ou na iminência do movimento — por exemplo, quando estamos parados sobre o solo ou quase nos movimentando. Já a força de atrito cinético, também chamado de dinâmico, atua sobre o corpo que está se movimentando — por exemplo, um carro se locomovendo em uma pista ou profissionais de patinação se deslocando no gelo.

Leia também: Força de atrito no plano inclinado

Fórmulas da força de atrito

• Força de atrito estático

\(\vec{f_{at}}= μ_e\cdot \vec{N}\)

• • \(\vec{f_{at}}\) é a força de atrito, medida em Newton [N].

  • \(μ_e\) é o coeficiente de atrito estático.

  • \( \vec{N}\) é a força normal, medida em Newton [N].

• Força de atrito cinético

\(\vec{f_{at}} = μ_c\cdot \vec{N}\)

• \(\vec{f_{at}}\) é a força de atrito, medida em Newton [N].

• \(μ_c\) é o coeficiente de atrito cinético.

• \( \vec{N}\) é a força normal, medida em Newton [N].

Como calcular a força de atrito?

Do ponto de vista matemático, a força de atrito é calculada por meio das suas fórmulas e sempre que for considerado o atrito entre os corpos. A seguir, veremos alguns exemplos de como calcular a força de atrito.

Exemplo 1: Uma pessoa está fazendo força sobre uma caixa que está quase se movimentando. Sabendo que o coeficiente de atrito estático vale 0,5 e a força normal é de 25 N, calcule a força de atrito da caixa.

Resolução:

Aqui, temos um caso de força de atrito estático, que calcularemos usando a fórmula:

\(\vec{f_{at}}= μ_e\cdot \vec{N}\)

\(\vec{f_{at}}= 0,5\cdot25\)

\(\vec{f_{at}}= 12,5\ N\)

A força de atrito nesse caso é de \(12,5\ N\).

Exemplo 2: Um carro se move em uma pista de coeficiente de atrito cinético igual a 0,8. Sabendo que a força normal é de 10 N, calcule a força de atrito entre o carro e a pista.

Resolução:

Aqui, temos um caso de força de atrito cinético, que calcularemos usando a fórmula:

\(\vec{f_{at}} = μ_c\cdot \vec{N}\)

\(\vec{f_{at}} = 0,8\cdot10\)

\(\vec{f_{at}} = 8\ N\)

A força de atrito nesse caso é de \(8\ N\).

Mapa mental: Força de atrito

* Para baixar o mapa mental em PDF, clique aqui!

Exercícios resolvidos sobre força de atrito

Questão 1

(PUC-RS) Sobre uma caixa de massa 120 kg, atua uma força horizontal constante F de intensidade 600 N. A caixa encontra-se sobre uma superfície horizontal em um local no qual a aceleração gravitacional é \(10\ m/s^2\). Para que a aceleração da caixa seja constante, com módulo igual a \(2\ m/s^2\), e tenha a mesma orientação da força F, o coeficiente de atrito cinético entre a superfície e a caixa deve ser de

a) 0,1

b) 0,2

c) 0,3

d) 0,4

e) 0,5

Resolução:

Alternativa C

Primeiramente, calcularemos a força normal, que é igual à força peso:

\(N=P\)

\(N=m\cdot g\)

\(N=120 \cdot 10\)

\(N=1200\)

Usando a segunda lei de Newton, conseguiremos encontrar o valor do coeficiente de atrito, em que F é maior que a força de atrito para que haja movimento:

\(F_R=m\cdot g\)

\(F – Fat=m\cdot a\)

\(600\ – μ_c\cdot1200=120\cdot2\)

\(600\ – μ_c\cdot1200=240\)

\( – μ_c\cdot1200=240-600\)

\(– μ_c\cdot1200=-360\)

\(– μ_c=\frac{-360}{1200}\)

\(– μ_c=-0,3\)

\( μ_c=0,3\)

Questão 2

(Enem) Uma pessoa necessita da força de atrito em seus pés para se deslocar sobre uma superfície. Logo, uma pessoa que sobe uma rampa em linha reta será auxiliada pela força de atrito exercida pelo chão em seus pés. Em relação ao movimento dessa pessoa, quais são a direção e o sentido da força de atrito mencionada no texto?

a) Perpendicular ao plano e no mesmo sentido do movimento.

b) Paralela ao plano e no sentido contrário ao movimento.

c) Paralela ao plano e no mesmo sentido do movimento.

d) Horizontal e no mesmo sentido do movimento.

e) Vertical e sentido para cima.

Resolução:

Alternativa C

Em relação ao movimento dos pés, a direção da força de atrito é paralela, e o sentido é o mesmo do movimento, já que ao pisarmos é feita uma força para trás, e o atrito nos empurra para frente.

Por Pâmella Raphaella Melo
Professora de Física

* Mapa Mental por Me. Rafael Helebrock