A força elétrica é a força que surge quando há duas cargas elétricas interagindo com os campos elétricos umas das outras. Calculamos sua intensidade usando a lei de Coulomb.
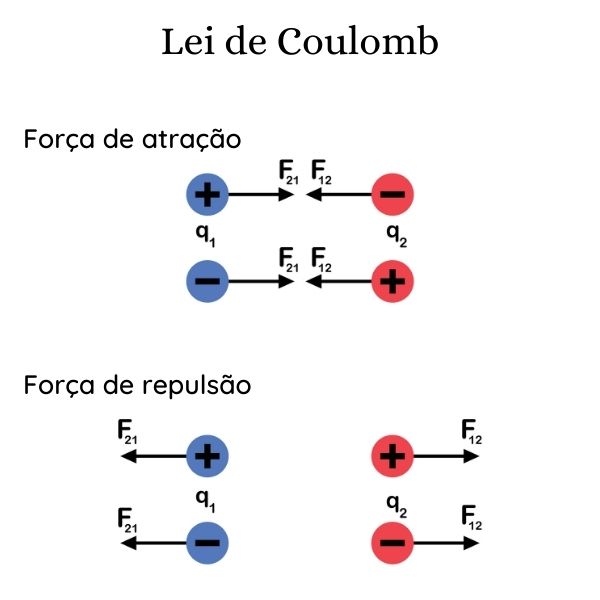
Sua direção se dá de acordo com a linha imaginária que une as cargas, e seu sentido varia de acordo com os sinais das cargas elétricas. Assim, quando \(q\geq0\), o sentido entre as forças é atrativo. Mas quando \(q<0\), o sentido entre as forças é repulsivo.
A lei de Coulomb, além de usada no cálculo da força, interliga essa força eletrostática com a distância ao quadrado entre as cargas e o meio em que estão inseridas. O trabalho da força elétrica pode ser encontrado pela quantidade de energia que a carga elétrica precisa para se locomover de um local a outro, independentemente do percurso escolhido.
Leia também: Como funciona a movimentação de cargas elétricas?
A força elétrica trata da interação entre as cargas elétricas.
A direção da força elétrica é a mesma da reta imaginária que conecta as cargas elétricas, possui sentido atrativo ou repulsivo dependendo dos sinais das cargas, e sua intensidade é calculada pela lei de Coulomb.
A lei de Coulomb associa a intensidade da força elétrica com a distância entre duas cargas elétricas.
Cargas elétricas de sinais iguais se atraem. Já cargas de sinais contrários se repelem.
O trabalho pode ser calculado pelo “esforço” que uma carga elétrica faz para se deslocar de um ponto a outro.
A força eletrostática, comumentemente chamada de força elétrica, faz parte das quatro interações fundamentais do universo, junto das forças nuclear forte, nuclear fraca e gravitacional. Ela aparece sempre que há um campo elétrico com carga elétrica em seu interior.
A orientação da força elétrica é a seguinte:
Direção: paralela à reta imaginária que liga as cargas elétricas.
Sentido: atrativo se as cargas tiverem mesmo sinal ou repulsivo se as cargas tiverem sinais opostos.
Intensidade: calculada pela lei de Coulomb.
A lei de Coulomb é o princípio físico responsável pela associação entre a força eletrostática e a distância entre duas cargas elétricas imersas no mesmo meio. Foi desenvolvida por Charles-Augustin de Coulomb (1736‒1806) em 1785.
Há uma relação de proporcionalidade entre a força e as cargas, mas a força é inversamente proporcional ao quadrado da distância, ou seja, se dobrarmos a distância, a força diminui \(\frac{1}{4}\) do seu valor original.
\(\vec{F}\propto\left|Q_1\right|\ e\left|Q_2\right|\)
\(\vec{F}\propto\frac{1}{d^2}\)
Vale ressaltar a importância que o sinal das cargas elétricas tem para determinar o sentido da força atuando entre elas, sendo atrativo para cargas de sinais contrários e repulsivo quando as cargas possuem sinais iguais.
A fórmula da lei de Coulomb é representada por:
\(\vec{F}=k\frac{\left|Q_1\right|\ \bullet\left|Q_2\right|}{d^2}\)
\(\vec{F}\) é a força de interação entre as partículas eletricamente carregadas, medida em Newton [N].
\(\left|Q_1\right|\) e \(\left|Q_2\right|\) são os módulos das cargas das partículas, medidos em Coulomb \([C]\).
d é a distância entre as cargas, medida em metros [m].
k é a constante eletrostática do meio, medida em \({\left(N\bullet m\right)^2/C}^2\).
Observação: A constante eletrostática muda de acordo com o meio em que as cargas estão.
O trabalho é a aplicação de uma força por um deslocamento, sendo irrelevante qual caminho foi percorrido, desde que partam do mesmo ponto em direção ao mesmo lugar.
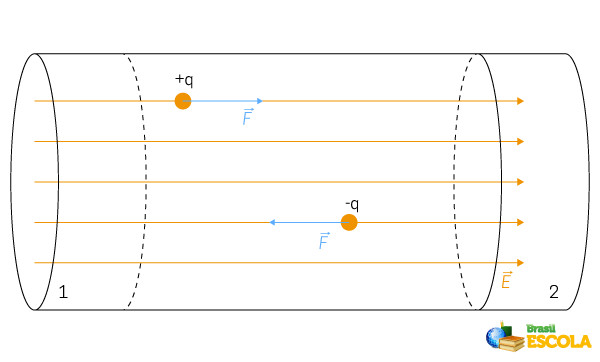
Em vista disso, o trabalho da força elétrica depende da força aplicada sobre uma carga elétrica para atravessar a distância do ponto 1 ao ponto 2, conforme a imagem.
Calculamos o trabalho por meio da fórmula:
\(W=\vec{F}\bullet d\bullet\cos{\theta}\)
W é o trabalho, medido em joules \([J]\).
d é a distância deslocada, medida em metros \([m]\).
θ é o ângulo entre \(\vec{F}e\ d,\), medido em graus.
Leia também: Eletrostática — área da Física destinada ao estudo das cargas em repouso
O campo elétrico ocorre nas redondezas de uma carga elétrica ou de uma superfície eletrizada, sendo uma propriedade intrínseca às cargas. A força elétrica surge quando há interação entre campos elétricos de no mínimo duas cargas elétricas, conforme demonstra a imagem.
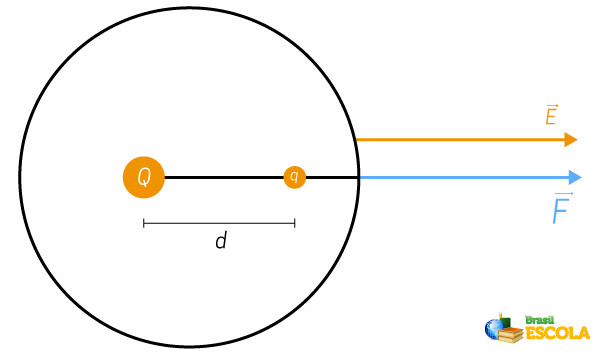
No que toca a orientação do campo elétrico com relação à força elétrica:
Direção: a mesma da força elétrica, ou seja, paralela à linha que une as cargas elétricas.
Sentido: o mesmo da força se \(q\geq0\), mas oposto ao da força se \(q<0\).
Intensidade: calculada pela fórmula do campo elétrico ou pela fórmula que relaciona força elétrica e campo elétrico, descrita abaixo:
\(\vec{F}=\left|q\right|\bullet\vec{E}\)
q é a carga elétrica, medida em coulomb \([C]\).
\(\vec{E}\) é o campo elétrico, medido em \([N/C]\).
Questão 1
(Mack-SP) Uma carga elétrica puntiforme com \(q=4,0\ \mu C\), que é colocada em um ponto P do vácuo, fica sujeita a uma força elétrica de intensidade \(1,2\ N\). O campo elétrico nesse ponto P tem intensidade:
a) \(3,0\bullet{10}^5\ N/C\)
b) \(2,4\bullet{10}^5\ N/C\)
c) \(1,2\bullet{10}^5\ N/C\)
d) \(4,0\bullet{10}^{-6}\ N/C\)
e) \(4,8\bullet{10}^{-6}\ N/C\)
Resolução:
Alternativa A
Como no enunciado o valor da força é fornecido e se pede o campo, podemos utilizar a forma que relaciona ambos:
\(\vec{F}=\left|q\right|\bullet\vec{E}\)
\(1,2=\left|4,0\ \mu\right|\bullet\vec{E}\)
Lembrando que \(\mu={10}^{-6}\), temos:
\(1,2=4,0\bullet{10}^{-6}\bullet\vec{E}\)
\(\frac{1,2}{4,0\bullet{10}^{-6}}=\vec{E}\)
\(0,3\bullet{10}^6=\vec{E}\)
\(3\bullet{10}^{-1}\bullet{10}^6=\vec{E}\)
\(3\bullet{10}^{-1+6}=\vec{E}\)
\(3\bullet{10}^5N/C=\vec{E}\)
Questão 2
Há uma carga elétrica de \(2,4\bullet{10}^{-4}\ C\) em um campo elétrico de \(6\bullet{10}^4\ N/C\) que se desloca 50 cm paralelamente ao eixo do campo. Qual é o trabalho que a carga realiza?
a) \(W=-7,2\ J\)
b) \(W=14,4\bullet{10}^{-2}\ J\)
c) \(W=7,2\bullet{10}^{-2}\ J\)
d) \(W=14,4\ J\)
e) \(W=7,2\ J\)
Resolução:
Alternativa E
Usando a fórmula que relaciona o trabalho e a força elétrica:
\(W=\vec{F}\bullet d\bullet\cos{\theta}\)
Como não foi dada a força elétrica, podemos fazer o cálculo usando o campo elétrico e a carga. Lembrando que como a carga é positiva, sua força e campo estão no mesmo sentido, então o ângulo entre a força e a distância deslocada é de 0°:
\(W=\left|q\right|\bullet\vec{E}\bullet d\bullet\cos{\theta}\)
\(W=\left|2,4\bullet{10}^{-4}\right|\bullet\left(6\bullet{10}^4\right)\bullet0,5\bullet\cos0°\)
\(W=14,4\bullet{10}^{-4+4}\bullet0,5\bullet1\)
\(W=14,4\bullet0,5\)
\(W=7,2\ J\)
Por Pâmella Raphaella Melo
Professora de Física
Fonte: Brasil Escola - https://brasilescola.uol.com.br/fisica/forca-eletrica.htm