Elementos de uma esfera
A esfera é um sólido geométrico formado pelo giro de 180° de uma circunferência. Seus elementos são secção, superfície, meridianos, entre outros.
Uma esfera é um sólido geométrico formado pelo giro de 180° de uma circunferência em torno do seu próprio eixo central, também chamado de eixo de rotação.
.jpg)
Note que a esfera também pode ser definida pelo giro de 360° de uma semicircunferência em torno de seu diâmetro. A imagem a seguir, à esquerda, mostra uma semicircunferência e seu diâmetro e, à direita, a esfera resultante de sua revolução (giro).
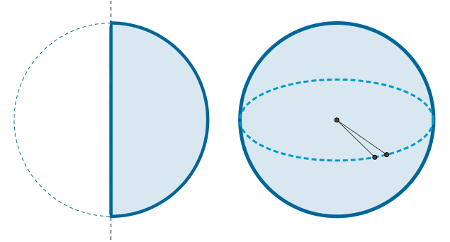
Elementos da esfera
-
Secção da esfera: é um corte feito na esfera por um plano. É a interseção entre a esfera e um plano. Qualquer interseção entre a esfera e o plano gera um círculo. Se esse plano passa pelo centro da esfera, além de gerar um círculo com o mesmo raio que o da esfera, esse círculo será o maior possível, chamado de círculo máximo.
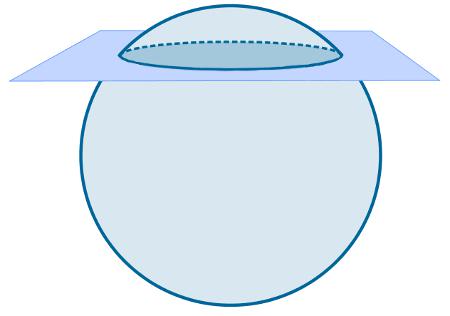
Para as secções transversais, vale a relação:
a2 = r2 + b2
- a é o raio da circunferência formada pela secção transversal;
- r é o raio da esfera;
- b é a distância do centro da esfera até a secção transversal.
-
Superfície esférica: é a “casca” da esfera. Pode ser obtida pelo giro de 360° de uma semicircunferência ao redor de seu diâmetro. É a parte da esfera usada para calcular sua área. Para esse cálculo, a fórmula usada é a seguinte:
A = 4πr2
*r é o raio da esfera.
-
Polos: o ponto “mais alto” e o“mais baixo” de uma esfera. São as interseções entre o diâmetro do semicírculo que foi girado e o sólido resultante.
-
Paralelo: é a circunferência observada na secção transversal da esfera com relação ao seu eixo de rotação.
Lembre-se: secção transversal da esfera é a secção perpendicular ao eixo de rotação dela.
-
Equador: É o paralelo cuja secção transversal passa pelo centro da esfera. Assim, é o maior paralelo e possui raio igual ao da esfera.
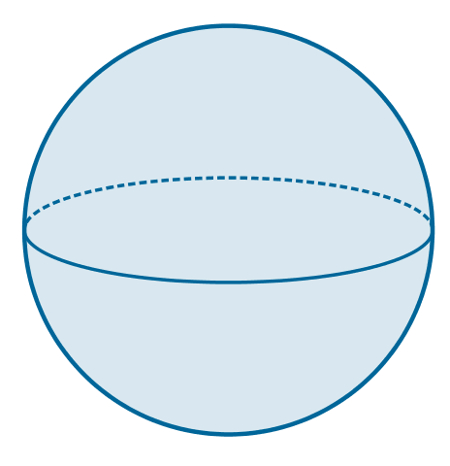
Exemplo de Equador
-
Meridiano: circunferência resultante da secção de uma esfera por um plano que contém seu eixo de rotação. De certa forma, podemos dizer que paralelos e meridianos são perpendiculares.
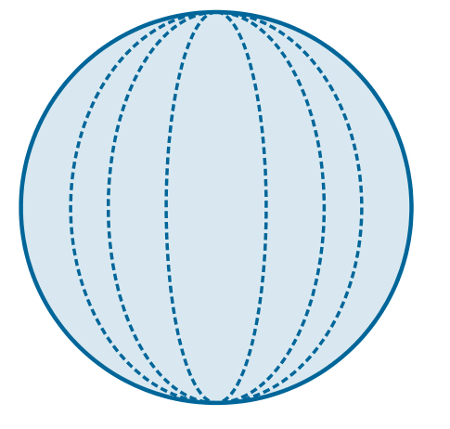
Exemplos de meridianos em uma esfera
Cunha esférica
Imagine, na definição de esfera, que um semicírculo não complete a volta de 360°. Digamos que ele dê uma volta de 30°. A figura será algo parecido com o objeto na figura a seguir:
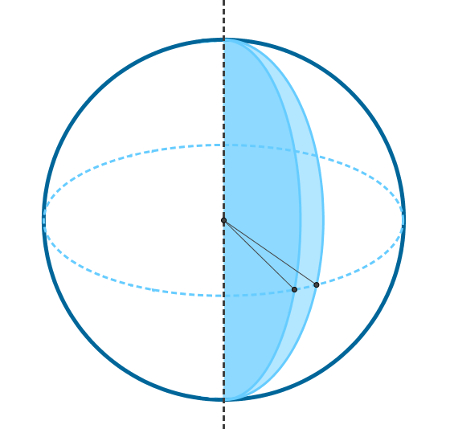
É possível calcular o volume da cunha esférica por meio de uma regra de três básica ou a partir de uma fórmula proveniente dessa regra. Para tanto, basta lembrar que o volume da esfera é resultado da revolução de um semicírculo em torno de seu próprio diâmetro em 360° e que a cunha esférica é resultado da mesma revolução apenas em α graus. Sendo V o volume da esfera e y o volume da cunha esférica, teremos:
V = y
360 α
Sabendo que V = 4/3πr3, teremos:
4/3πr3 = y
360 α
360y = α4πr3
3
y = α4πr3
3·360
y = απr3
270
Fuso esférico
É equivalente à cunha esférica, mas para uma semicircunferência. Um exemplo de fuso esférico pode ser encontrado na figura a seguir.
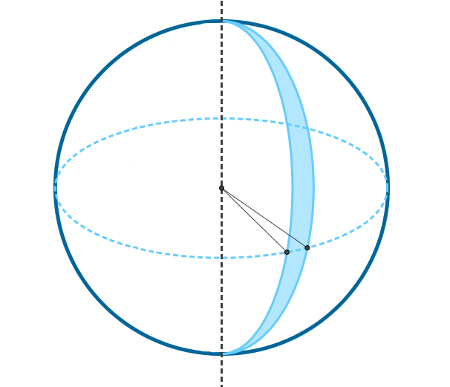
Também podemos calcular a área do fuso esférico por meio de uma regra de três. Para tanto, lembre-se de que a área da superfície esférica completa é resultado de uma revolução em 360° de uma circunferência e que a área do fuso é uma revolução em α graus de uma circunferência. Como a área da superfície completa é A = 4πr2, a área do fuso esférico é x e pode ser calculada da seguinte maneira:
4πr2 = x
360 α
Resolvendo a equação, teremos:
360x = α4πr2
x = 4απr2
360
x = απr2
90
Exemplo
Calcule a área e o volume de uma parte da laranja, sabendo que o raio da esfera da laranja é de 4 centímetros e que o ângulo dessa parte é de 90°.
Para calcular o volume, utilizamos a fórmula dada ou regra de três:
y = απr3
270
y = 90·3,14·43
270
y = 282,6·64
270
y = 18086,4
270
y = 67 cm3
Para calcular a área, basta utilizar a respectiva fórmula.
x = απr2
90
x = 90·3,14·42
90
x = 282,6·16
90
x = 4521,6
90
x = 50,24 cm2
Por Luiz Paulo Moreira
Graduado em Matemática
Fonte: Brasil Escola - https://brasilescola.uol.com.br/matematica/elementos-uma-esfera.htm