Ondulatória

Ondulatória é uma área da Física que investiga o comportamento das ondas e oscilações. Por meio do seu estudo, é possível compreender as características, os elementos e as classificações das ondas e oscilações, permitindo prever o seu comportamento com base em apenas algumas informações.

Leia também: O que são ondas gravitacionais?

Resumo sobre ondulatória

• A ondulatória é um ramo da Física que se ocupa do estudo das ondas e oscilações.
• De acordo com a natureza da onda, as ondas periódicas podem ser mecânicas ou eletromagnéticas.
• De acordo com a direção de vibração, as ondas podem ser transversais ou longitudinais.
• De acordo com o número de dimensões de propagação, as ondas podem ser unidimensionais, bidimensionais ou tridimensionais.
• Na ondulatória estudamos os elementos de onda: crista da onda, vale da onda, comprimento de onda, amplitude da onda, período da onda, frequência da onda, e velocidade de propagação da onda.

O que a ondulatória estuda?

A ondulatória estuda o comportamento das ondas e oscilações, permitindo compreender suas características, propriedades e os fenômenos ondulatórios.

Quais são os tipos de ondas na ondulatória?

Na ondulatória, as ondas podem ser classificadas com base na sua natureza, na direção de sua vibração, e no número de dimensões da propagação da sua energia.

-> De acordo com a natureza da onda

A natureza da onda pode ser mecânica, eletromagnética ou de matéria. As ondas mecânicas são aquelas que somente se propagam em meios materiais (ar, água e metais), como são as ondas em uma corda ou ondas sonoras. As ondas eletromagnéticas são aquelas que se propagam tanto em meios materiais como em meios não materiais (vácuo), como as micro-ondas e raios ultravioletas. As ondas de matéria são aquelas associadas aos átomos, às moléculas e às partículas subatômicas.

-> De acordo com a direção de vibração da onda

A direção de vibração da onda pode ser:

• longitudinal;
• transversal.

As ondas longitudinais são aquelas que oscilam paralelamente a sua direção de propagação, como as ondas do ultrassom e ondas sonoras. As ondas transversais são aquelas que oscilam perpendicularmente a sua direção de propagação, como as ondas em uma corda e as ondas luminosas.

-> De acordo com o número de dimensões da propagação da energia das ondas

O número de dimensões da propagação da energia das ondas pode ser:

• unidimensional;
• bidimensional;
• tridimensional.

As ondas unidimensionais são aquelas que vibram em apenas uma única dimensão, como as ondas de uma corda. As ondas bidimensionais são aquelas que vibram em duas dimensões, como as ondas do mar. As ondas trimensionais são aquelas que vibram em três dimensões, como as ondas luminosas.

-> Videoaula sobre a classificação das ondas na ondulatória

Quais são os elementos da ondulatória?

Os elementos da ondulatória são crista da onda, vale da onda, comprimento de onda, amplitude da onda, período da onda, frequência da onda e velocidade de propagação da onda, como podemos ver a sua representação na imagem abaixo:

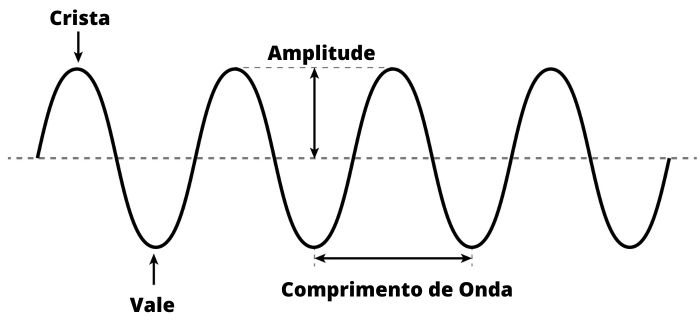
• Crista da onda: são os pontos máximos em cada onda.
• Vale da onda: são os pontos mínimos em cada onda.
• Comprimento de onda: é o intervalo dado por uma crista e um vale de onda, duas cristas consecutivas de uma onda ou dois vales consecutivos de uma onda.
• Amplitude da onda: é a altura máxima que a onda atinge, dada pela diferença entre a crista da onda ou o vale da onda até a posição de equilíbrio.
• Período da onda: é o intervalo de tempo que leva para a conclusão de um comprimento de onda.
• Frequência da onda: é a quantidade de oscilações que uma onda realiza em determinado tempo.
• Velocidade de propagação da onda: é a velocidade com a qual a onda se desloca em um meio, por exemplo, a velocidade da onda de luz no vácuo é de aproximadamente 3∙10⁸ m/s  e a velocidade da onda sonora no nível do mar é de aproximadamente 340 m/s .

Saiba mais: Cinco coisas sobre as ondas que você precisa saber

Fórmulas da ondulatória

-> Fórmula do período da onda

\(T=\frac{1}{f}\)

Em que:

T é o período, medido em segundos s .

f é a frequência, medida em Hertz [Hz] .

Pode ser representada também por:

 \(T=\frac{∆t }{n}\)

Em que:

T é o período, medido em segundos s .

∆t é a variação de tempo, medida em segundos [s] .

n é o número de oscilações.

-> Fórmula da frequência da onda

\(f=\frac{1}{T}\)

Em que:

f é a frequência, medida em Hertz [Hz] .

T é o período, medido em segundos s .

Pode ser representada também por:

\(f=\frac{n}{∆t}\)

Em que:

f é a frequência, medida em Hertz [Hz] .

n é o número de oscilações.

∆t é a variação de tempo, medida em segundos [s] .

-> Fórmula da velocidade de propagação da onda

\(v=\lambda\cdot f\)

Em que:

v é a velocidade de propagação da onda, medida em [m/s] .

λ é o comprimento de onda, medido em metros [m] .

f é a frequência, medida em Hertz [Hz] .

Pode ser representada também por:

\(v=\frac{\lambda}{T}\)

Em que:

v é a velocidade de propagação da onda, medida em [m/s] .

λ é o comprimento de onda, medido em metros [m] .

T é o período, medido em segundos s .

-> Equação de Taylor (ondas em uma corda)

\(v=\sqrt{\frac{F}{m}}\)

Em que:

v é a velocidade de propagação da onda, medida em [m/s] .

F é a intensidade da força de tração na corda, medida em Newton [N] .

m é a massa da corda, medida em quilograma [kg] .

Exemplo 1:

Calcule o período de uma onda que possui uma frequência de 500 Hz.

Calcularemos o período pela fórmula:

\(T=\frac{1}{f}\)

\(T=\frac{1}{500}\)

\(T=0,002\ s\)

Então o período dessa onda é de 0,002 s .

Exemplo 2:

Determine a velocidade de propagação de uma onda, sabendo que o seu comprimento de onda é de 4 metros e a sua frequência é de 300 Hz.

Calcularemos a velocidade da onda pela fórmula:

\(v=\lambda\cdot f\)

\(v=4\cdot300\)

\(v=1200\ m/s\)

Então a velocidade de propagação da onda é de 1200 m/s .

Exercícios resolvidos sobre ondulatória

Questão 1 (Enem) As notas musicais podem ser agrupadas de modo a formar um conjunto. Esse conjunto pode formar uma escala musical. Dentre as diversas escalas existentes, a mais difundida é a escala diatônica, que utiliza as notas denominadas dó, ré, mi, fá, sol, lá e si. Essas notas estão organizadas em ordem crescente de alturas, sendo a nota dó a mais baixa e a nota si a mais alta. Considerando uma mesma oitava, a nota si é a que tem menor

a) amplitude.

b) frequência.

c) velocidade.

d) intensidade.

e) comprimento de onda.

Resolução:

Alternativa E. A nota si é a mais alta, sendo a mais aguda, com isso, ela possui maior frequência e oscilação e menor comprimento de onda.

Questão 2 (Enem) A corrida dos 100 m rasos é uma das principais provas do atletismo e qualifica o homem mais rápido do mundo. Um corredor de elite foi capaz de percorrer essa distância em 10 s, com 41 passadas. Ele iniciou a corrida com o pé direito. O período de oscilação do pé direito desse corredor foi mais próximo de
a) 1/10 s.

b) 1/4 s.

c) 1/2 s.

d) 2 s.

e) 4 s.

Resolução:

Alternativa C. Calcularemos o período de oscilação dos pés por meio da divisão do tempo total da prova pela quantidade de passadas:

 \(T=\frac{tempo\ total\ da\ prova}{número\ de\ passadas}\)

\(T=\frac{10}{41}\)

\(T\cong0,244\ s\)

Para calcularmos o período de oscilação do pé direito, basta multiplicar o resultado anterior por 2, então:

\(T\cong0,244\cdot2\)

\(T\cong0,487\)

\(T\cong\frac{1}{2}\ s\)

Fontes

NUSSENZVEIG, Herch Moysés. Curso de física básica: Fluidos, Oscilações e Ondas, Calor (vol. 2). 5 ed. São Paulo: Editora Blucher, 2015.

HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos da Física: Gravitação, Ondas e Termodinâmica (vol. 2) 8. ed. Rio de Janeiro, RJ: LTC, 2009.

Por Pâmella Raphaella Melo
Professora de Física