Momento de uma força

O momento de uma força (torque) é o responsável pelo movimento de rotação de um corpo quando empregamos uma força em um braço de alavanca. A sua direção e sentido são definidos pela regra da mão direita e o seu módulo é calculado por meio da sua fórmula.

Leia também: Afinal, o que é força?

Resumo sobre o momento de uma força

• O momento de uma força (torque) é o responsável pelo movimento de rotação.
• Calculamos o momento de uma força por meio do produto entre a força aplicada, a distância do eixo e o seno do ângulo formado entre eles.
• O momento angular é diretamente proporcional ao momento de uma força.
• A rotação de um corpo ocorre ao aplicarmos uma força em um ponto de maneira que a linha de ação dessa força produza um momento de uma força ao redor do ponto ou eixo de rotação.

O que é momento de uma força?

Também chamado de torque, o momento de uma força é uma grandeza física vetorial que ocorre sempre que aplicamos uma força em um braço de alavanca (distância até o eixo de rotação), fazendo com que o corpo rotacione.

Quanto mais longe for o braço de alavanca de um corpo, mais facilmente ele será rotacionado, como descrito na imagem a seguir:

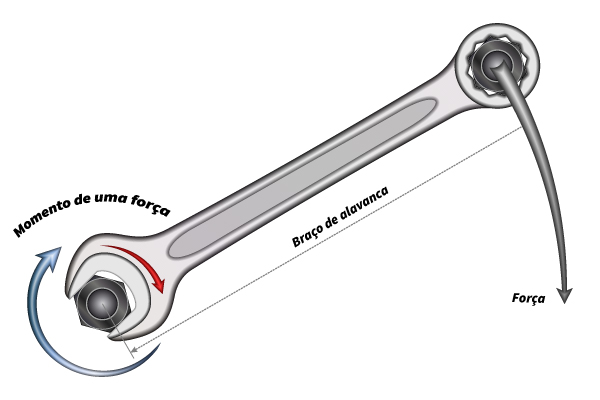
Como o momento de uma força é uma grandeza vetorial, sua direção, sentido e módulo são dados por:

• Direção e sentido: dados pela regra da mão direita. O dedão representa o momento de uma força, e a mão curvada, a aplicação da força.
• Módulo: dado pela sua fórmula. O momento de uma força terá sinal negativo quando o movimento for no sentido horário e sinal positivo quando o momento for no sentido anti-horário.

Fórmula do momento de uma força

\(\tau = r\cdot F \cdot sen\theta\)

• \(\tau\) → momento de uma força ou torque produzido, medido em [N·m].
• r → distância do eixo de rotação, também chamada de braço de alavanca, medida em metros [m].
• F → força produzida, medida em Newton [N].
• θ → ângulo entre a distância e a força, medido em graus [°].

Quando o ângulo for de 90º, a fórmula de torque pode ser representada por:

\(\tau = r\cdot F\)

• \(\tau\) → momento de uma força ou torque produzido, medido em [N·m].
• r → distância do eixo de rotação, também chamada de braço de alavanca, medida em metros [m].
• F → força produzida, medida em Newton [N].

Como calcular o momento de uma força?

O momento de uma força (torque) pode ser calculado por meio da sua fórmula. Abaixo vemos um exemplo de como se calcula o momento de uma força.

• Exemplo:

Calcule o momento de uma força sobre uma maçaneta circular cujo eixo de rotação encontra-se em seu centro, tem diâmetro de 5 cm e é girada no sentido horário por uma força de 100 N.

Resolução:

Primeiramente, converteremos a distância de centímetros para metros:

5 cm = 0,02 m

Depois, calcularemos o momento de uma força ou torque por meio da sua fórmula geral:

\(\tau = r\cdot F \cdot sen\theta\)

\(\tau = 0,05\cdot 100 \cdot sen30º\)

\(\tau = 0,05\cdot 100 \cdot 0,5\)

\(\tau= - 2,5 N\cdot m \)

O sinal negativo do momento de uma força ocorre porque a maçaneta gira no sentido horário.

Veja também: Como fazer o cálculo do momento de uma força (torque) de uma chave de roda?

Momento de uma força x momento angular

Quando há uma situação de equilíbrio de rotação, em que a soma de todos os momentos de uma força (torque) é nula, o momento angular mantém-se constante. O momento angular é uma grandeza física relacionada à rotação do corpo, sendo diretamente proporcional ao momento de uma força, de modo que, à medida que aumentamos o momento angular, aumentamos também o momento de uma força.

O momento angular pode ser calculado de duas maneiras distintas: pelo momento de uma força (torque) ou pela sua relação com o momento linear:

\(\tau = \frac{\Delta L}{\Delta t}\)

• \(\tau\)→ momento de uma força ou torque produzido, medido em [N∙m].
• \(\Delta L\) → variação do momento angular, medida em [kg·m²/s].
• \(\Delta t\) → variação de tempo, medida em segundos [s].

\(L=r\cdot p\cdot sen\theta \)

• L → momento angular, medido em [kg·m²/s].
• r  → distância entre o objeto e o eixo de rotação ou raio, medida em metros [m].
• p  → momento linear, medido em [kg·m/s].
• θ  → ângulo entre o r e Q , medido em graus [°].

A fórmula do momento linear é:

\(p=m\cdot v\)

• p  → momento, medido em [kg·m/s].
• m  → massa, medida em quilogramas [kg].
• v  → velocidade, medida em metros por segundo [m/s].

Momento de uma força em relação a um eixo

Para que ocorra a rotação de um corpo, é necessário aplicar uma força em um ponto de maneira que a linha de ação dessa força produza um momento de uma força (ou torque) ao redor do ponto ou eixo de rotação.

Exercícios resolvidos sobre momento de uma força

Questão 1

(Enem) Em um experimento, um professor levou para a sala de aula um saco de arroz, um pedaço de madeira triangular, e uma barra de ferro cilíndrica e homogênea. Ele propôs que fizessem a medição da massa da barra utilizando esses objetos. Para isso, os alunos fizeram marcações na barra, dividindo-a em oito partes iguais, e em seguida apoiaram-na sobre a base triangular, com o saco de arroz pendurado em uma de suas extremidades, até atingir a situação de equilíbrio.

Nessa situação, qual foi a massa da barra obtida pelos alunos?

A) 3,00 kg

B) 3,75 kg

C) 5,00 kg

D) 6,00 kg

E) 15,00 kg

Resolução:

Alternativa E.

Para o sistema ficar em equilíbrio, precisamos calcular a massa da barra por meio da igualdade entre os momentos de uma força:

\(\tau_1 = \tau_2\)

\(F_1\cdot r_1=F_2\cdot r_2\)

Na barra e no saco de arroz estão atuando a força peso, então:

\(P_{arroz}\cdot r_1=P_{barra}\cdot r_2\)

A barra está a uma posição de distância do eixo, e o arroz, a três posições de distância do eixo:

\(m_{arroz}\cdot g\cdot 3=m_{barra}\cdot g\cdot 1\)

\(5\cdot 3=m_{barra}\cdot 1\)

\(15=m_{barra}\)

\(m_{barra}=15 kg\)

Questão 2

Um encanador aplica uma força de 1000 N a 0,5 m do braço de alavanca com um ângulo de 30º em relação ao braço de alavanca para girar uma manivela no sentido anti-horário. Qual é o valor do momento de uma força gerado?

Dados: sen 30º = 0,5 e cos 30º = 0,9.

A) 50 N·m

B) 100 N·m

C) 150 N·m

D) 200 N·m

E) 250 N·m

Resolução:

Alternativa E. 

Calcularemos o momento de uma força por meio da sua fórmula:

\(\tau = r\cdot F \cdot sen\theta\)

\(\tau = 0,5\cdot 1000 \cdot sen30º\)

\(\tau = 0,5\cdot 1000 \cdot 0,5\)

\(\tau=250 N\cdot m \)

Fontes

HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos da Física: Mecânica. 8. ed. Rio de Janeiro, RJ: LTC, 2009.

NUSSENZVEIG, Herch Moysés. Curso de física básica: Mecânica (vol. 1). 5 ed. São Paulo: Editora Blucher, 2015.