Centro de massa

O centro de massa é um ponto crucial para a estabilidade dos corpos, evitando que eles tombem. O centro de massa de um corpo ou de um sistema de partículas é o ponto geométrico de que podemos tratar como se toda a massa do corpo estivesse nele. O seu cálculo depende da massa e da posição das partículas.

Leia também: Afinal, o que é massa?

Resumo sobre o centro de massa

• O centro de massa é um ponto crucial para a estabilidade dos corpos, evitando que eles tombem.
• O centro de massa é o ponto calculado através da média ponderada da posição das partículas com suas massas.
• O centro de massa e o centro de gravidade coincidem em figuras e corpos geométricos regulares.
• O centro de massa, a velocidade do centro de massa e a aceleração do centro de massa são calculados através de uma média ponderada.
• A análise do centro de massa é importante para a estabilidade de tombamento.
• O centro de massa pode ser usado como um sistema de referência.

O que é centro de massa?

O centro de massa é um ponto crucial para a estabilidade dos corpos, evitando que eles tombem.

Ele pode ser definido da seguinte forma:

(...) o ponto que se move como se toda a massa do sistema estivesse concentrada nesse ponto e todas as forças externas estivessem aplicadas nesse ponto.

HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos da Física: Mecânica. 8. ed. Rio de Janeiro, RJ: LTC, 2009.

Então, podemos compreender o centro de massa como o local que representa a posição média ponderada de toda a massa do sistema.

O centro de massa precisa ser levado em consideração nas construções de pontes, edifícios, casas, móveis, automóveis, portas, janelas; enfim, tudo aquilo que necessita de equilíbrio.

Fórmula do centro de massa

\(x_{CM}=\frac{m_1\cdot x_1+m_2\cdot x_2+m_3\cdot x_3}{m_1+m_2+m_3}\)

• x_CM → posição do centro de massa do sistema de partículas no eixo horizontal.
• m₁, m₂  e m₃ → massas das partículas.
• x₁, x₂  e x₃ → posições das partículas no eixo horizontal.
• y₁, y₂  e y₃ → posições das partículas no eixo vertical.

E

\(y_{CM}=\frac{m_1\cdot y_1+m_2\cdot y_2+m_3\cdot y_3}{m_1+m_2+m_3}\)

• y_CM → posição do centro de massa do sistema de partículas no eixo vertical.
• m₁, m₂  e m₃ → massas das partículas.
• x₁, x₂  e x₃ → posições das partículas no eixo horizontal.
• y₁, y₂  e y₃ → posições das partículas no eixo vertical.

Como calcular o centro de massa de um objeto?

Para calcular o centro de massa de um objeto ou sistema de partículas, calculamos a posição do centro de massa no eixo horizontal e depois no eixo vertical, o que nos dará um par de coordenadas correspondente ao centro de massa do objeto ou sistema.

• Exemplo:

Qual a posição do centro de massa de um sistema de partículas de 1 kg posicionado nos pontos P1 = (0,2); P2 = (1,4); P3 = (5,3)?

Resolução:

Primeiramente, calcularemos o centro de massa no eixo x:

\(x_{CM}=\frac{m_1\cdot x_1+m_2\cdot x_2+m_3\cdot x_3}{m_1+m_2+m_3}\)

\(x_{CM}=\frac{1\ \cdot\ 0\ +\ 1\ \cdot\ 1\ +\ 1\ \cdot\ 5}{1\ +\ 1\ +\ 1}\)

\(x_{CM}=\frac{0\ +\ 1\ +\ 5}{3}\)

\(x_{CM}=\frac{6}{3}\)

\(x_{CM}=2\)

Por fim, calcularemos o centro de massa no eixo y:

\(y_{CM}=\frac{m_1\cdot y_1+m_2\cdot y_2+m_3\cdot y_3}{m_1+m_2+m_3}\)

\(y_{CM}=\frac{1\ \cdot\ 2\ +\ 1\ \cdot\ 4\ +\ 1\ \cdot\ 3}{1\ +\ 1\ +\ 1}\)

\(y_{CM}=\frac{2\ +\ 4\ +\ 3}{3}\)

\(y_{CM}=\frac{9}{3}\)

\(y_{CM} = 3\)

O centro de massa desse sistema de partículas está na posição (2,3).

Centro de massa x centro de gravidade

É comum confundir os termos centro de massa com centro de gravidade, mas eles não são o mesmo conceito. O centro de gravidade (ou baricentro) é um ponto fixo no corpo ou em um sistema em que temos a ação de toda a força da gravidade. Já o centro de massa é um ponto no corpo ou em um sistema que se comporta como se toda sua massa estivesse concentrada nele.

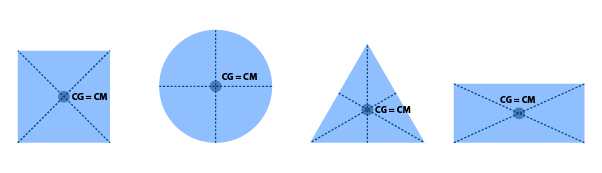
Em figuras e corpos geométricos regulares como quadrados, triângulos e círculos, o centro de gravidade coincide com o centro de massa; nos demais geralmente não coincidem. Para saber mais sobre o centro de gravidade, clique aqui.

Velocidade do centro de massa

A velocidade do centro de massa pode ser dada por uma operação vetorial que relaciona o somatório do vetor quantidade de movimento de cada partícula com o somatório da massa das partículas, representada pela fórmula:

\(\vec{v}_{CM} = \frac{\sum \vec{p}}{\sum m} = \frac{\vec{p}_1 + \vec{p}_2 + \vec{p}_3 + \cdots}{m_1 + m_2 + m_3 + \cdots} \)

• \(\vec{v}_{CM}\) → vetor  velocidade do centro de massa do sistema de partícula.
• \(\vec{p}\) → vetor quantidade de movimento.
• m  → massa da partícula.
• \(\vec{p}_1, \vec{p}_2 \ e\ \vec{p}_3\) → vetores quantidade de movimento das partículas.
• m₁, m₂ e m₃ → massas das partículas.

Ou:

\(\vec{v}_{CM} = \frac{\sum m \cdot \vec{v}}{\sum m} = \frac{m_1 \cdot \vec{v}_1 + m_2 \cdot \vec{v}_2 + m_3 \cdot \vec{v}_3 + \cdots}{m_1 + m_2 + m_3 + \cdots}\)

• \(\vec{v}_{CM}\) → vetor  velocidade do centro de massa do sistema de partícula.
• m  → massa da partícula.
• \(\vec{v}\) → vetor velocidade
• m₁, m₂ e m₃ → massas das partículas.
• \(\vec{v}_1,\vec{v}_2 \ e\ \vec{v}_3 ​ \) → vetores velocidade das partículas.

Aceleração do centro de massa

A aceleração do centro de massa é dada por uma operação vetorial que relaciona o somatório do vetor força de cada partícula com o somatório da massa das partículas, representada pela fórmula:

\(\vec{a}_{CM} = \frac{\sum \vec{F}}{\sum m} = \frac{\vec{F}_1 + \vec{F}_2 + \vec{F}_3 + \cdots}{m_1 + m_2 + m_3 + \cdots}\)

• \(\vec{a}_{CM}\) → vetor aceleração do centro de massa do sistema de partícula.
• \(\vec{F}\) → vetor força da partícula.
• m → massa da partícula.
• \(\vec{F}_1,\vec{F}_2 \ e\ \vec{F}_3 ​ \) → vetores força das partículas.
• m₁, m₂ e m₃ → massas das partículas.

Ou

\(\vec{a}_{\text{CM}} = \frac{\sum m \cdot \vec{a}}{\sum m} = \frac{m_1 \cdot \vec{a}_1 + m_2 \cdot \vec{a}_2 + m_3 \cdot \vec{a}_3 + \cdots}{m_1 + m_2 + m_3 + \cdots}\)

• \(\vec{a}_{CM}\) → vetor  aceleração do centro de massa do sistema de partícula.
• m  → massa da partícula.
• \(\vec{a}\) → vetor aceleração da partícula.
• m₁, m₂ e m₃ → massas das partículas.
• \(\vec{a}_1,\vec{a}_2 \ e\ \vec{a}_3 ​ \) → vetores aceleração das partículas.

Centro de massa e estabilidade de tombamento

Através do centro de massa é possível obtermos o ângulo máximo que um corpo consegue se inclinar sem que haja o seu tombamento. Uma das maneiras para descobrirmos isso é calculando as posições do centro de massa nos eixos e depois empregando conhecimentos trigonométricos. Haverá tombamento quando a posição do centro de massa passar a sua projeção na base de apoio.

O centro de massa pode ser usado como um sistema de referência para análise dos movimentos dos corpos rígidos, corpos em sistemas isolados ou em sistemas de partículas. Ao empregarmos o centro de massa como sistema de referência temos a simplificação dos problemas físicos, já que o centro de massa passa a ser a origem do sistema de coordenadas.

Exercícios resolvidos sobre centro de massa

Questão 1

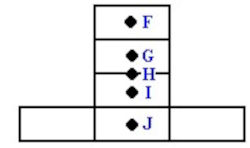
(Cesgranrio) Seis peças de um jogo de dominó estão dispostas como na figura. Dos pontos indicados (F, G, H, I, J), o que melhor localiza o centro de massa desse conjunto é:

A) F

B) G

C) H

D) I

E) J

Alternativa D.

Primeiramente, delimitaremos um eixo vertical e um horizontal na figura:

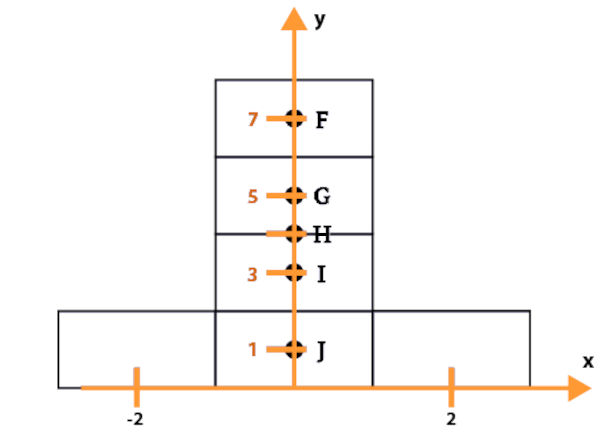
Os centros de cada bloco são: bloco 1 = (-2,1), bloco 2 = (0,1), bloco 3 = (2,1), bloco 4 = (0,3), bloco 5 = (0,5), bloco 6 = (0,7). O centro de massa no eixo x será o ponto no meio dos 3 pontos, portanto no ponto zero.

Por fim, calcularemos o centro de massa no eixo y através da sua fórmula:

\( y_{\text{CM}} = \frac{m_1 \cdot y_1 + m_2 \cdot y_2 + m_3 \cdot y_3 + m_4 \cdot y_4 + m_5 \cdot y_5 + m_6 \cdot y_6}{m_1 + m_2 + m_3 + m_4 + m_5 + m_6} \)

\(y_{\text{CM}} = \frac{m \cdot 1 + m \cdot 1 + m \cdot 1 + m \cdot 3 + m \cdot 5 + m \cdot 7}{m + m + m + m + m + m} \)

\(y_{CM}=\frac{18m}{6m}\)

\(y_{CM}=3\)

Então, o centro de massa desse sistema fica no ponto (0,3), que corresponde à letra I.

Questão 2

Determine a velocidade do centro de massa de um sistema de partículas de 2 kg posicionado com vetor velocidade (0,-2) e (1,-4).

A) 4 ;-0,5 m/s

B) 3 ;-0 m/s

C) 2 ;-1 m/s

D) 1 ;-2 m/s

E) 0,5 ;-3 m/s

Alternativa E.

Calcularemos a velocidade do centro de massa através da fórmula:

\( \vec{v}_{\text{CM}} = \frac{m_1 \cdot \vec{v}_1 + m_2 \cdot \vec{v}_2 + m_3 \cdot \vec{v}_3 + \cdots}{m_1 + m_2 + m_3 + \cdots}\)

\(\vec{v}_{\text{CM}} = \frac{2\ \cdot\ (0, -2) + 2\ \cdot\ (1, -4)}{2 + 2} \)

\(\vec{v}_{\text{CM}} = \frac{(0, -4) + (2, -8)}{4} \)

\(\vec{v}_{\text{CM}} = \frac{(0 + 2, -4 - 8)}{4} \)

\(\vec{v}_{\text{CM}} = \frac{(2, -12)}{4} \)

\(\vec{v}_{\text{CM}} = (0,5\ ; -3) \, \text{m/s} \)

Fontes

HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos da Física: Mecânica. 8. ed. Rio de Janeiro, RJ: LTC, 2009.

NUSSENZVEIG, Herch Moysés. Curso de física básica: Mecânica (vol. 1). 5 ed. São Paulo: Editora Blucher, 2015.