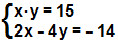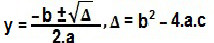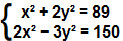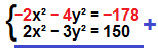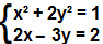PUBLICIDADE
Os sistemas de equações nada mais são do que estratégias que nos permitem resolver problemas e situações que envolvem mais de uma variável e pelo menos duas equações. Se as equações presentes no sistema envolverem apenas a adição e a subtração das incógnitas, dizemos que se trata de um sistema de equações do 1° grau. Podemos resolver esse sistema de duas formas, através da representação gráfica ou algebricamente. Na forma algébrica, dispomos de duas alternativas, o método da adição ou da substituição.
No caso de uma multiplicação entre as incógnitas ou, simplesmente, de uma delas aparecer como uma potência de expoente 2, dizemos que o sistema envolve também equações de 2° grau. Para resolver um sistema desse tipo, as estratégias são as mesmas citadas anteriormente, mas podem haver mais soluções nesse caso.
Vejamos alguns exemplos de resolução de sistemas de equações do 1° e do 2° grau:
1° Exemplo:
Observe que, nesse exemplo, a equação x·y = 15 fornece um produto entre as incógnitas x e y, portanto, essa é uma equação do 2° grau. Para resolvê-la, vamos utilizar o método da substituição. Na segunda equação, isolaremos x:
2x – 4y = – 14
2x = 4y – 14
x = 4y – 14
2
x = 2y – 7
Agora substituiremos x = 2y – 7 na primeira equação:
x·y = 15
(2y – 7)·y = 15
2y² – 7y – 15 = 0
Para encontrar os possíveis valores de y, utilizaremos a fórmula de Bhaskara:
Δ = b² – 4.a.c
Δ = (– 7)² – 4.2.(– 15)
Δ = 49 + 120
Δ = 169
y = – b ± √Δ
2.a
y = – (– 7) ± √169
2.2
y = 7 ± 13
4
|
y1 = 7 + 13 |
y2 = 7 – 13 |
Agora podemos substituir os valores encontrados para y em x·y = 15 com o objetivo de determinar os valores de x:
|
x1 · y1 = 15 |
x2 · y2 = 15 |
Podemos afirmar que a equação possui duas soluções do tipo (x, y), são elas: (3, 5) e (– 10, – 3/2).
2° Exemplo:
Para resolver esse sistema, utilizaremos o método da adição. Para tanto, vamos multiplicar a primeira equação por – 2. Nosso sistema ficará da seguinte forma:
(– 2x² + 2x²) + (– 4y² – 3y²) = (– 178 + 150)
0x² – 7y² = – 28
7y² = 28
y² = 28
7
y = ±√4
y1 = + 2
y2 = – 2
Agora nós podemos substituir os valores encontrados para y na primeira equação com o objetivo de obter os valores de x:
| x² + 2y1² = 89 x² + 2.(2)² = 89 x² + 8 = 89 x² = 81 x = ±√81 x1 = + 9 x2 = – 9 |
x² + 2y2² = 89 x² + 2.(– 2)² = 89 x² + 8 = 89 x² = 81 x = ±√81 x3 = + 9 x4 = – 9 |
Podemos afirmar que a equação possui quatro soluções: (9, 2), (– 9, 2), ( 9, – 2) e (– 9, – 2).
3° Exemplo:
Na resolução desse sistema de equações, utilizaremos o método da substituição. Na segunda equação, vamos isolar x:
2x – 3y = 2
2x = 3y + 2
x = 3y + 2
2
x = 3y + 1
2
Substituiremos x na primeira equação:
x² + 2y² = 1
(3y/2 + 1)² + 2y² = 1
9y² + 3y + 1 + 2y² = 1
4
Multiplicaremos toda a equação por 4:
9y² + 12 y + 4 + 8y² = 4
17y² + 12 y = 0
Para encontrar os possíveis valores de y, vamos utilizar a fórmula de Bhaskara:
Δ = b² – 4.a.c
Δ = 12² – 4.17. 0
Δ = 144
y = – b ± √Δ
2.a
y = – 12 ± √144
2.17
y = – 12 ± 12
34
| Y1 = – 12 + 12 34 y1 = 0 34 y1 = 0 |
y2 = – 12 – 12 34 y2 = – 24 34 y2 = – 12 17 |
Substituindo os valores encontrados para y em 2x – 3y = 2, podemos determinar os valores de x:
| 2x – 3y1 = 2 2x – 3·0 = 2 2x – 0 = 2 x = 2 2 x1 = 1 |
2x – 3y2 = 2 2x – 3·(– 12/17)= 2 2x + 36 = 2 17 2x = 2 – 36 17 2x = – 2 17 x2 = – 1 17 |
Podemos afirmar que a equação possui duas soluções do tipo (x, y), são elas: (1, 0) e (– 1/17, – 12/17).
Por Amanda Gonçalves
Graduada em Matemática