Polígonos

Polígonos são figuras geométricas planas e fechadas formadas por segmentos de reta. Os polígonos dividem-se em dois grupos, os convexos e os não convexos. Quando um polígono possui todos os seus lados iguais e, consequentemente, todos os ângulos internos iguais, trata-se de um polígono regular. Os polígonos regulares podem ser nomeados de acordo com a quantidade de seus lados.

Veja também: Construção de polígonos circunscritos

Elementos de um polígono

Polígono é a figura plana e fechada formada pela união de um número finito de segmentos de retas. Assim, considere um polígono qualquer:

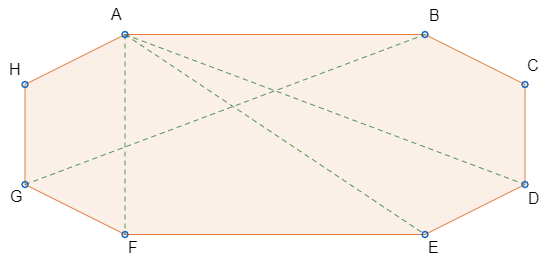
Os pontos A, B, C, D, E, F, G e H são os vértices do polígono e são formados pelo encontros dos segmentos AB, BC, CD, DE, EF, FG, GH e HA, chamados lados do polígono.

Os segmentos AF, AE, AD e BG são as diagonais do polígono. (Perceba que esses são alguns exemplos de diagonais, no polígono anterior temos mais dessas.) Diagonais são segmentos de retas que “ligam” os vértices do polígono.

Nomenclatura de um polígono

Podemos nomear os polígonos de acordo com seu número de lados. Veja na tabela a seguir o nome dos principais polígonos.

Note que não é necessário decorar a tabela e sim entendê-la. Com exceção do triângulo e do quadrilátero, a formação da palavra é:

Número de lados + gono

Por exemplo, quando temos o polígono de cinco lados, automaticamente nos lembramos do prefixo penta mais o sufixo gono: pentágono.

Exemplo

Determine o nome do polígono a seguir:

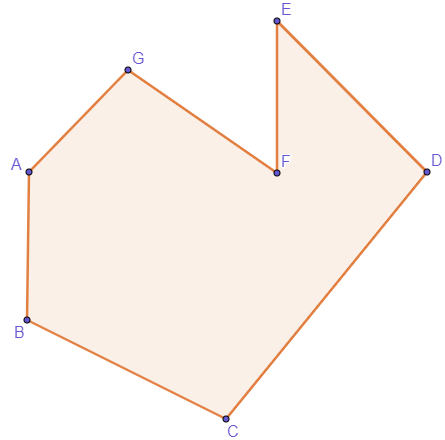
Classificação dos polígonos

Os polígonos são classificados pela medida de seus ângulos e lados. Um polígono é dito equilátero quando possui lados congruentes, ou seja, todos lados iguais; e será dito equiângulo quando possuir ângulos congruentes, isto é, todos ângulos iguais.

Caso um polígono seja equilátero e equiângulo, então ele será um polígono regular.

Em todo polígono regular, o centro tem a mesma distância dos lados, ou seja, é equidistante dos lados. O centro do polígono é também o centro da circunferência inscrita no polígono, ou seja, a circunferência que está “dentro” da circunferência.

Leia mais: Semelhança de polígonos: veja quais são as condições

Soma dos ângulos internos de um polígono

Seja a_i um ângulo interno de um polígono regular de n lados, representaremos a soma desses ângulos internos por S_i.

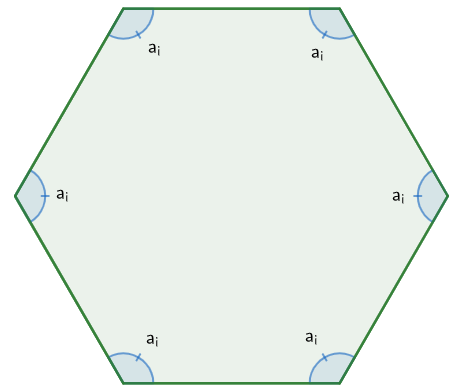
Assim, a soma dos ângulos internos é dada por:

S_i = (n - 2) · 180°

Para calcular o valor de cada ângulo interno, basta pegar o valor da soma dos ângulos internos e dividir pelo número de lados, ou seja:

a_i = S_i
       n

Exemplo 1

Determine a soma dos ângulos internos e, em seguida, a medida de cada ângulo interno de um icoságono.

Sabemos que um icoságono possui vinte lados, logo, n = 20. Substituindo nas relações, temos:

S_i = (n - 2) · 180°

S_i = (20 - 2) · 180°

S_i = 18 · 180°

S_i = 3240°

Agora, para determinar o valor de cada ângulo interno, basta dividir o valor encontrado pelo número de lados:

a_i = 3240°
    20

a_i = 162°

Exemplo 2

A soma dos ângulos internos de um polígono regular é 720°, determine o polígono.

Substituindo a informação do enunciado na fórmula, temos:

720° = (n - 2) · 180°

720° = 180n – 360°

180n = 720° + 360°

180n = 1080°

n = 1080°
      180°

n = 6 lados

Assim, o polígono procurado é o hexágono.

Soma dos ângulos externos de um polígono

A soma dos ângulos externos de um polígono é sempre igual a 360°.

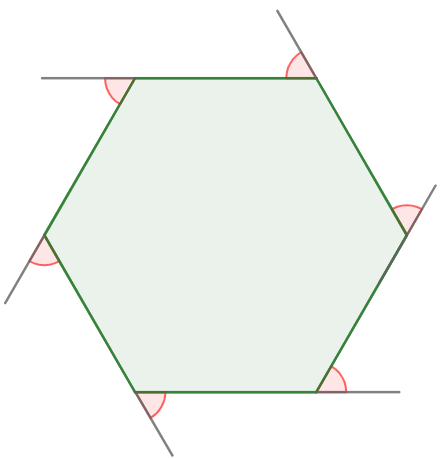
S_e = 360°

a_e = S_e
         n

a_e = 360°
      n

Diagonais dos polígonos

Considere um polígono de n lados. Para determinar o número de diagonais (d), utilizamos a seguinte relação:

d = n · (n - 3)
     2

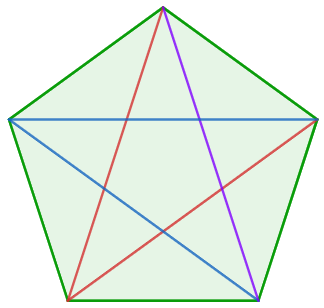
Exemplo

Determine o número de diagonais de um pentágono e represente-as graficamente.

Sabemos que um pentágono possui cinco lados, assim, n = 5. Substituindo na expressão, temos que:

d = 5 · (5 - 3)
      2

d = 5 · 2
      2

d = 5

Área e perímetro dos polígonos

O perímetro de polígonos é definido pela soma de todos os lados. A área de um polígono é calculada a partir da divisão do polígono em figuras cujo cálculo da área é mais fácil, como o triângulo e o quadrado.

A_Δ = base · altura
        2

A_quadrado = base · altura

Exemplo

Determine uma expressão matemática que represente a área de um hexágono regular.

Solução:

Inicialmente, considere um hexágono regular e todos os segmentos de retas que liguem o centro do polígono a cada vértice. Assim:

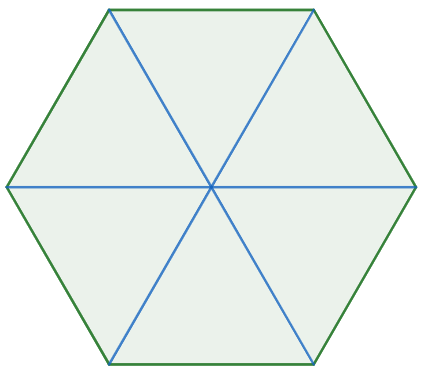
Perceba que, devido ao fato do hexágono ser regular, ao dividi-lo, encontramos seis triângulos equiláteros, logo, a área do hexágono é seis vezes a área do triângulo equilátero, ou seja:

A_hexágono = 6 · A_Δ

A_hexágono = 6 · l² · √3
                         4

A_hexágono = 3 · l² · √3
                         2

A_hexágono = 3 · l²·√3
                          2

Leia também: Área do triângulo equilátero

Exercícios resolvidos

Questão 1 – (Enem) Uma piscina tem o formato de um polígono regular cuja medida do ângulo interno é três vezes e meia a medida do ângulo externo. Qual é a soma dos ângulos internos do polígono cuja forma é igual à dessa piscina?

a) 1800°

b) 1620°

c) 1440°

d) 1260°

e) 1080°

Solução

Como não sabemos a quantidade de lados do polígono, vamos imaginar só um dos vértices desse polígono.

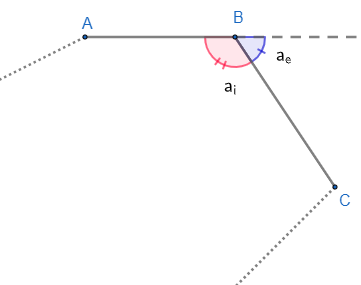
Da imagem podemos ver que:

a_i + a_e = 180° (I)

Do enunciado temos que:

a_i = 3,5 · a_e (II)
 

Substituindo a equação (II) na equação (I), teremos que:

3,5 · a_e + a_e = 180°

4,5 · a_e = 180°

a_e = 180°
       4,5

a_e = 40°

No entanto sabemos que um ângulo interno é a divisão de 360° pelo número de lados do polígono. Assim:

a_e = 360°
      n

40° = 360°
        n

40n = 360°

n = 360°
      40°

n = 9

Logo, a soma dos ângulos internos da piscina é:

S_i = (n - 2) · 180°

S_i = (9 - 2) · 180°

S_i = 7 · 180°

S_i = 1260° 

Por Robson Luiz
Professor de Matemática

Gostaria de fazer a referência deste texto em um trabalho escolar ou acadêmico? Veja:

LUIZ, Robson. "Polígonos"; Brasil Escola. Disponível em: https://brasilescola.uol.com.br/matematica/poligonos.htm. Acesso em 19 de outubro de 2021.