PUBLICIDADE
Considere dois números complexos quaisquer:
![]()
1. Multiplicação
O produto de z1 por z2 será dado por:
![]()
Observe que o número complexo resultante é tal que:
Seu módulo é igual ao produto dos módulos de z1 e z2 e seu argumento é igual à soma dos argumentos de z1 e z2.
Importante: Esse procedimento pode ser generalizado para a multiplicação de n números complexos:
![]()
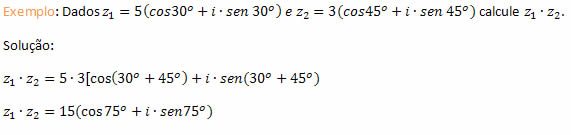
2. Divisão
O quociente entre z1 e z2 será dado por:
![]()
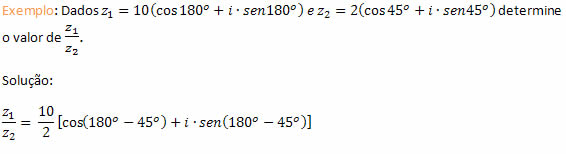
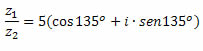
Não pare agora... Tem mais depois da publicidade ;)
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática
Equipe Brasil Escola





