PUBLICIDADE
A divisão de fração, embora pareça ser uma operação complicada, é algo muito simples de resolver. É importante lembrar que, para resolver essa operação, é necessário que lembremos como ocorre a multiplicação de fração.
Leia também: Adição e subtração de frações
Aqui, vamos nos dedicar a explicar passo a passo de como fazer uma divisão entre duas ou mais frações. Além disso, vamos entender a partir de elementos gráficos o algoritmo da divisão de frações.

Tópicos deste artigo
- 1 - Como fazer uma divisão de fração
- 2 - Como representar uma divisão de frações
- 3 - Exercícios resolvidos
Como fazer uma divisão de fração
Para realizarmos a operação de divisão de frações, é necessário entendermos antes a operação de multiplicação entre frações. Para multiplicar duas ou mais frações, basta multiplicar o numerador com numerador e, em seguida, denominador com denominador. Veja o exemplo a seguir:
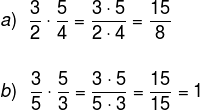
Agora precisamos entender a ideia de divisão entre uma fração e um número inteiro. Para isso, vamos mostrar como representar graficamente uma fração.
Nosso objetivo é dividir a fração ½ por 4. Sabemos que um meio representa algo inteiro divido em duas partes, ou seja, cada parte será 1 dividido por 2, então:
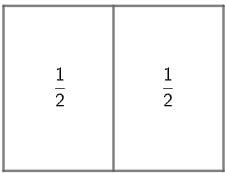
Perceba que procuramos dividir cada uma das 2 partes (½) em 4 partes. Note que, se observarmos a quantidade de partes formadas em relação ao retângulo inteiro, teremos 8 partes, logo cada uma das partes será representada por 1/8. Veja a figura a seguir:
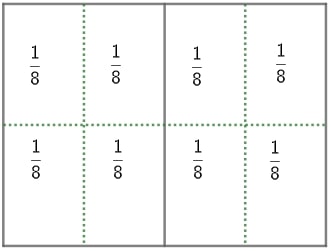
Assim, o resultado da divisão 1/2 por 4 é igual a um 1/8.
Veja que, quando partimos o retângulo que estava dividido em 2 partes em 4, ou seja, dividimos a fração 1/2 por 4, obtemos a fração 1/8. Realizar essa operação de divisão, portanto, é o mesmo que realizar a multiplicação a seguir:
![]()
A fim de facilitar o cálculo da divisão de fração, podemos adotar essa ideia fazendo a seguinte generalização:
Para fazer a divisão entre frações, basta manter a primeira fração e multiplicá-la pelo inverso da segunda.
Exemplo:
a) Vamos dividir a fração 2/3 pela fração 5/6:
![]()
b) Determine o quociente entre os números um centésimo e um milésimo.
![]()
Como representar uma divisão de frações
Podemos representar a divisão de frações de duas formas.
A primeira forma e a mais comum delas é:
![]()
Podemos representar uma divisão de frações também da seguinte maneira:
![]()
Leia também: Problemas envolvendo números fracionários
Exercícios resolvidos
Questão 1 - Determine o resultado da divisão a seguir:
![]()
Solução:
De acordo com o algoritmo, devemos manter a primeira fração e multiplicar pelo inverso da segunda fração, assim:
![]()
Questão 2 – Represente graficamente a divisão a seguir:
![]()
Solução:
Para realizar a representação gráfica dessa divisão de frações, devemos representar a fração 1/8 e contar quantas partes deram em relação à fração um ½ . Veja:
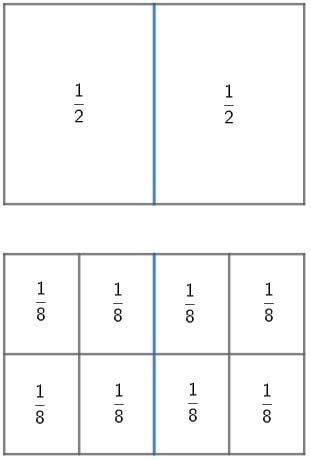
Perceba que, quando olhamos para fração um 1/8 em relação à fração um ½, temos 4 partes de um 1/8 dentro de um 1/2. Assim,
![]()
Por Robson Luiz
Professor de Matemática





