PUBLICIDADE
Com três pontos distintos e não alinhados formamos um plano, para que com eles seja formada uma reta é preciso que eles estejam alinhados.
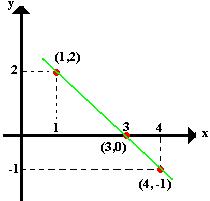
Considere os pontos A(1,2), B(3,0), C(4,-1). Colocando-os em um plano cartesiano percebemos que a união irá formar uma reta, ou seja, eles estão alinhados.
Unir os três pontos distintos em um plano cartesiano é uma opção para verificar seu alinhamento, mas isso nem sempre apresenta uma resposta segura, pois um dos três pontos pode estar milímetros fora da reta formada, o que deixa os três pontos não alinhados.
Por esse motivo, ao verificar se os três pontos são alinhados, é preciso seguir a seguinte condição:
Os pontos A, B e C pertencem à reta formada acima e o ponto B é comum aos segmentos AB e BC, nesse caso podemos aplicar a seguinte propriedade: Duas retas paralelas que possuem um ponto em comum são coincidentes.
Unindo essa propriedade com o cálculo dos coeficientes, iremos concluir que os pontos A, B e C serão paralelos se o coeficientes dos dois segmentos mAB e mBC forem iguais.
mAB = 0 – 2 = – 2 = – 1
3 – 1 2
MBC = – 1 – 0 = –1 = – 1
4 – 3 1
Como mAB = mBC podemos dizer que os três (A, B e C) pontos estão alinhados.
Analisando esse exemplo chegamos à seguinte condição de alinhamento de três pontos:
Dado três pontos distintos A (xA, yB), B (xB,yB) e C (xC, yC), eles serão alinhados se, somente se, os coeficientes mAB e mBC forem iguais.
Por Danielle de Miranda
Graduada em Matemática