Área do setor circular

Setor circular é uma região do círculo delimitada por dois raios do círculo e um arco da circunferência. O setor circular é como se fosse uma fatia da circunferência.

Para calcular a área do setor circular, é comum recorrermos à regra de três, pois a área será proporcional ao ângulo existente entre os raios que delimitam esse setor. Portanto, é necessária a medida do ângulo ou do comprimento do arco e também do comprimento do raio.

r/2.· = c_sr²/ 360°. Já a área do setor circular, considerando-se o comprimento do arco (c), é calculada por A·πθ· = _sa área do setor circular pode ser calculada por Ae o raio (r), )θConsiderando o ângulo (

Leia também: Círculo e circunferência — qual a diferença?

Resumo sobre área do setor circular

• Setor circular é a região do círculo delimitada por dois raios e um arco.

• Para calcular a área do setor circular, conhecendo seu ângulo central, utiliza-se a fórmula:

• Para calcular a área do setor circular, conhecendo o comprimento do arco (c), utiliza-se a fórmula:

O que é setor circular?

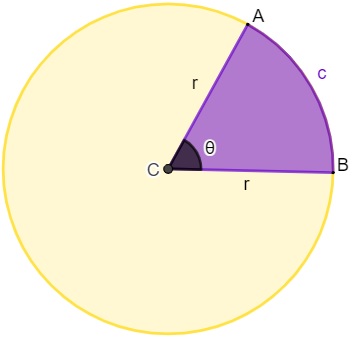
Conhecemos como setor circular a região de um círculo fechada por dois raios e um arco. O setor circular é como se fosse uma fatia do círculo.

• C → centro da circunferência;

• r → comprimento do raio do círculo;

• θ → ângulo central;

• c → comprimento do arco.

Casos particulares de setor circular

Existem alguns casos particulares de setor circular. Trata-se da metade, do quadrante e do octante.

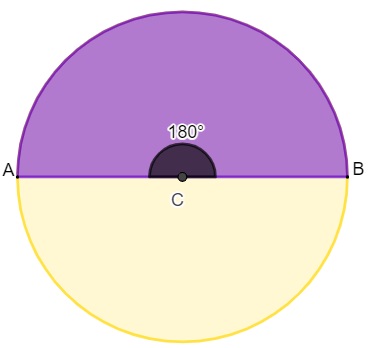
• Metade: é formada nos casos em que o setor circular é igual à metade do círculo, ou seja, o ângulo central é de 180º.

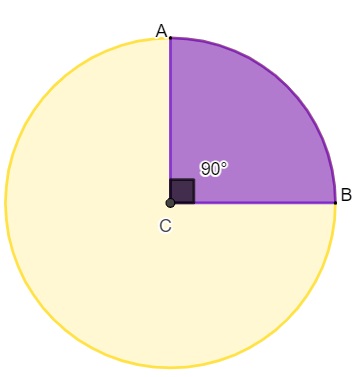
• Quadrante: é a área correspondente a um quarto do círculo, com ângulo central de 90°.

• Octante: é a área correspondente à oitava parte de um círculo. Nesse caso, o ângulo central é de 45°.

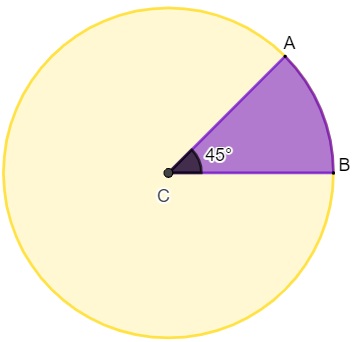
Como calcular a área de um setor circular?

É possível calcular a área do setor circular em função de seu ângulo central ou em função do comprimento de seu arco.

• Cálculo da área do setor circular em função do ângulo central

Para calcular a área do setor circular A_s, é necessário conhecer a medida do ângulo central desse setor e o raio do círculo. A área do setor circular sempre será proporcional ao ângulo θ. Sabe-se que a área total do círculo é igual a πr². Logo, podemos fazer a seguinte relação:

πr² → 360°

A_s → θ

Conhecendo os valores de r e de θ, é possível encontrar o valor da área do setor circular. A partir dessa regra de três é que podemos deduzir também a fórmula para o cálculo da área do setor. Multiplicando de forma cruzada, temos que:

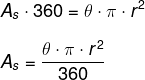
Exemplo:

Calcule a área do setor circular a que possui ângulo central de 30°, sabendo que o raio do círculo é de 4 cm.

Resolução:

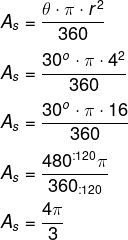
• Cálculo da área do setor circular em função do comprimento do arco

Para calcular a área do setor circular em função do comprimento do arco c, basta lembrar que o comprimento da circunferência, C = 2πr, corresponde à área total do círculo. Como a área do setor é proporcional, correlaciona-se:

πr² → 2πr

A_s → c

Multiplicando de forma cruzada, obtém-se que:

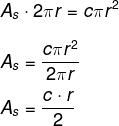
Exemplo:

Calcule a área do setor circular, sabendo que o comprimento do arco é de 20 cm e o raio é de 12 cm.

A_s = 20 · 15 : 2

A_s = 300 : 2

A_s = 150 cm²

Leia também: Como encontrar o centro de uma circunferência?

Exercícios resolvidos sobre área do setor circular

Questão 1

A área do setor circular a seguir é de: (use π = 3)

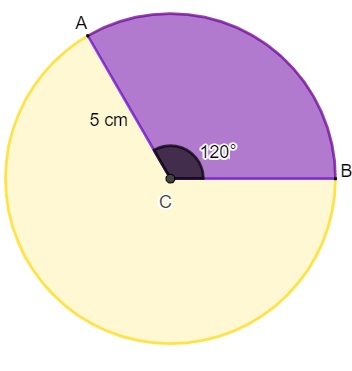
A) 12 cm².

B) 15 cm².

C) 25 cm².

D) 50 cm².

E) 65 cm².

Resolução:

Alternativa C

Sabe-se que θ = 120°, r = 5 e também que π = 3. Então, tem-se o seguinte cálculo:

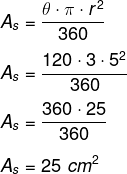
Questão 2

A área do setor circular que é limitada por um arco que possui comprimento igual à sexta parte de π e pertence a um círculo que possui 12 cm de raio é igual a:

A) 0,5π cm².

B) 0,75π cm².

C) π cm².

D) 1,5π cm².

E) 2π cm².

Resolução:

Alternativa C

Considerando que c = π : 6 e que r = 12, obtém-se o seguinte:

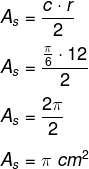
Por Raul Rodrigues de Oliveira
Professor de Matemática

Gostaria de fazer a referência deste texto em um trabalho escolar ou acadêmico? Veja:

OLIVEIRA, Raul Rodrigues de. "Área do setor circular"; Brasil Escola. Disponível em: https://brasilescola.uol.com.br/matematica/area-setor-circular.htm. Acesso em 23 de janeiro de 2022.