Área da pirâmide

A área de uma pirâmide é uma medida relacionada com a sua superfície. As pirâmides possuem um polígono qualquer, chamado de base, e faces laterais triangulares. Assim, a área da pirâmide (A) é a soma entre a área de sua base (A_B) e a área de suas faces laterais (A_L). Em outras palavras:

A = A_B + A_L

A área das faces laterais de uma pirâmide é obtida pela soma de todas as áreas de cada uma de suas faces laterais.

Cada caso deve ser analisado separadamente, pois as pirâmides nem sempre são regulares e de base quadrada, como as do Egito. Quando uma pirâmide é regular, podemos calcular a área de apenas uma face lateral e multiplicar o resultado pelo número total de faces laterais para encontrar A_L.

Veja um exemplo de cálculo de área da pirâmide regular.

Exemplo

Vamos calcular a área de uma pirâmide regular quadrangular que possui as seguintes medidas: a aresta da base mede 18 cm e a altura mede 12 cm.

Como essa pirâmide é regular, basta calcular a área de uma face lateral e multiplicar esse resultado por 4 (número de faces laterais) para obter A_L. Para isso, precisamos calcular a apótema dessa pirâmide. Isso pode ser feito pelo teorema de Pitágoras:

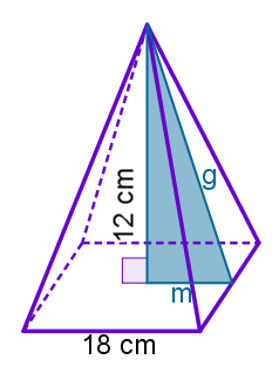
Observe na imagem acima que g é a apótema da pirâmide e m é a apótema da base. Com a altura, essas medidas formam um triângulo retângulo. A medida de m é 9 cm, pois a extremidade da altura de uma pirâmide regular coincide com o centro do quadrado. Assim, por Pitágoras:

g² = 9² + 12²

g² = 81 + 144

g² = 225

g = √225

g = 15

A apótema da pirâmide regular é a altura de suas faces laterais. A área de uma face lateral é a área do triângulo cuja altura (apótema) mede 15 cm e cuja base mede 18 cm:

A_F1 = 15·18
         2

A_F1 = 270
         2

A_F1 = 135 cm²

A área total das faces laterais é igual a quatro vezes a área de apenas uma delas, pois a pirâmide é regular:

A_F = 4A_F1 = 4·135

A_F = 540

Falta ainda calcular a área da base dessa pirâmide. Como ela é quadrada e sua aresta mede 18 cm teremos:

A_B = 18²

A_B = 324 cm²

A área da pirâmide é dada por:

A = A_B + A_L

A = 324 + 540

A = 864 cm²

Se a pirâmide não for regular, é necessário calcular cada uma das faces laterais e somá-las para depois calcular a área da base.

Por Luiz Paulo Moreira
Graduado em Matemática